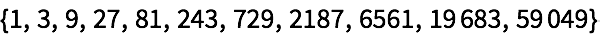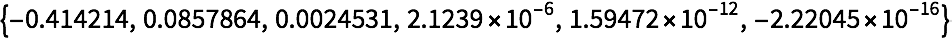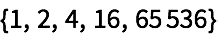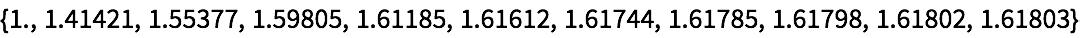| 27 | Aplicación repetida de funciones |
f[x] aplica
f a
x.
f[f[x]] aplica
f a
f[x]; de hecho, anida la aplicaci
ón de
f. Es usual que se quiera repetir o anidar una funci
ón.
Aqu
í se forma una lista con los resultados de anidar
f 4 veces:
Si la funci
ón que se usa es
Framed, resulta un poco m
ás obvio lo que est
á sucediendo:
Cuando se quiere ver la lista de los resultados de anidaciones sucesivas, se usa
NestList. Si solo interesa el resultado final, se usa
Nest.
Aquí aparece el resultado final de 5 niveles de anidación:
Aplique
EdgeDetect de manera anidada a una imagen encontrando: primero, bordes, luego bordes de los bordes, y as
í sucesivamente.
Detecte en una imagen bordes, de manera anidada:
Use una funci
ón pura para detectar, en cada paso, los bordes y al mismo tiempo dar el negativo de color:
Comenzando con el rojo, mezcle con amarillo de manera anidada, a modo de obtener cada vez m
ás amarillo.
A
ñada a la mezcla otro amarillo en cada paso:
Si se aplica sucesivamente una función que suma 1, se obtienen enteros sucesivos.
Sume 1 de manera anidada, para obtener n
úmeros sucesivos:
Multiplique por 2 de manera anidada, para obtener potencias de 2.
El resultado se duplica cada vez, dando una lista de las potencias de 2:
Si se eleva al cuadrado de manera anidada, se alcanzan n
úmeros grandes muy r
ápidamente:
Tambi
én se pueden anidar las ra
íces cuadradas.
Aplique la raíz cuadrada de manera anidada:
La versi
ón decimal del resultado converge r
ápidamente (a la
razón áurea):
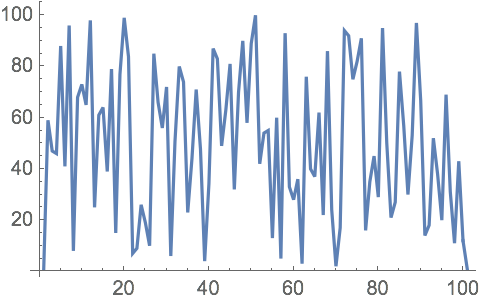
RandomChoice elige al azar de una lista. Esto puede usarse, por ejemplo, para crear una funci
ón pura que sume al azar +1 o
−1.
En cada paso, sume o reste 1, al azar, comenzando de 0:
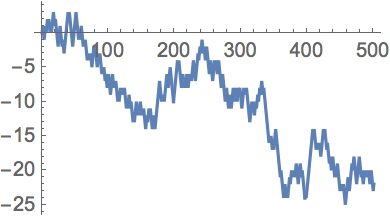
Aqu
í se generan 500 pasos de una
“caminata aleatoria
”:
Hasta ahora se ha usado
NestList iterativamente, de hecho, para efectuar una cadena de aplicaciones de una funci
ón dada. Ahora bien, tambi
én puede usarse para fines de
recursión, donde lo que se anida es el patr
ón mismo de aplicaciones de la funci
ón.
Aquí se efectúa una cadena de aplicaciones de la función f:
Aquí el patrón de aplicaciones de f es más complicado:
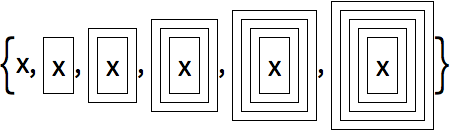
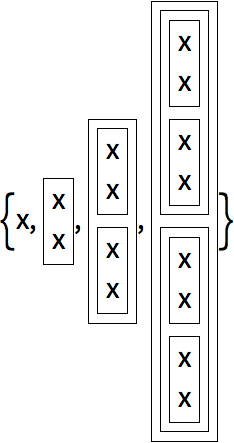
Si se enmarcan los resultados se podr
á entender mejor lo que est
á sucediendo:
Si se acomoda todo en columnas, se deja ver el patr
ón anidado de aplicaciones de la funci
ón.
En cada nivel, las cajas anidadas se combinan en pares, de manera recursiva:
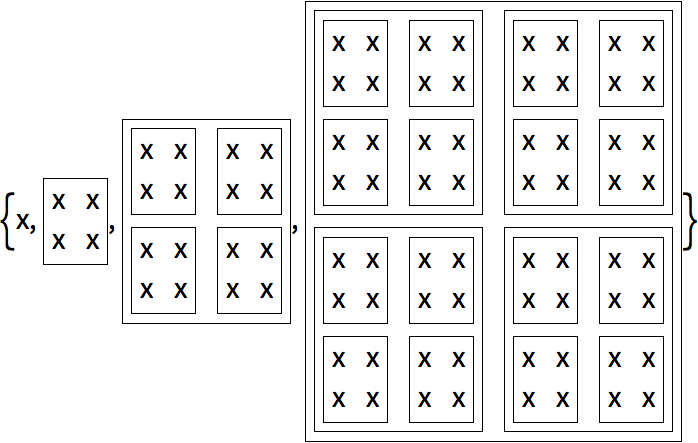
A continuaci
ón, una secuencia de rejillas anidadas de manera recursiva:
Aqu
í se forma el comienzo de una estructura fractal:
Pueden obtenerse sin dificultad estructuras de tipo recursivo muy vistosas:
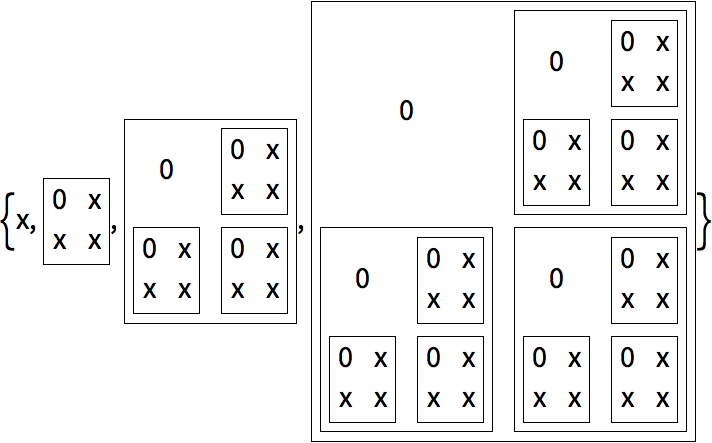
No todos los resultados de una recursi
ón son tan complicados. He aqu
í un ejemplo donde se suman sucesivamente dos copias desplazadas de una lista, como en
{0,1,2,1}+{1,2,1,0}.
A
ñada, al principio y al final, un 0 a una lista y, luego, sume los resultados:
Si el resultado se acomoda en una rejilla, se va formando el
triángulo de Pascal de los coeficientes binomiales:
Aqu
í se muestra otro ejemplo de recursi
ón con
NestList.
Forme una estructura recursiva con dos funciones, f y g:
Es bastante complicado entender la estructura así formada, aun si se acomodan las cosas en columnas.
Acomodar en columnas la estructura recursiva:
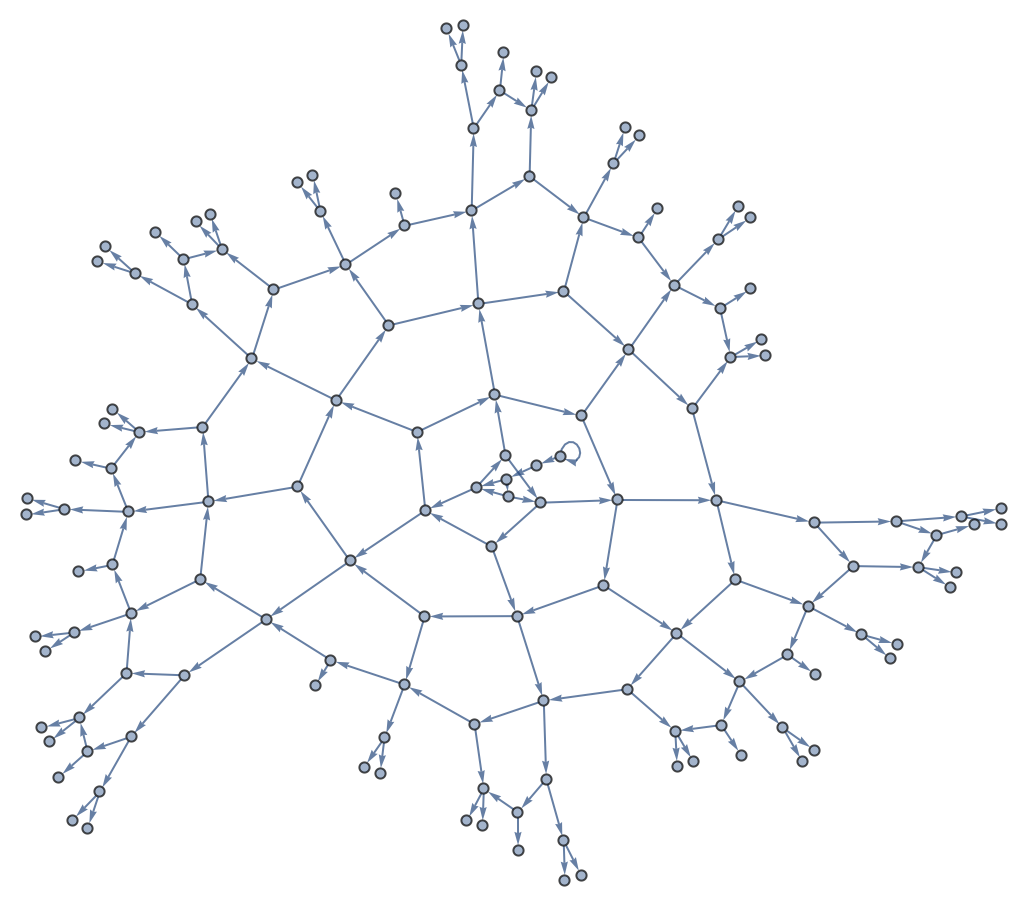
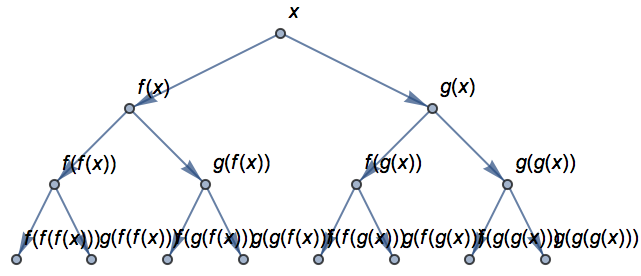
NestGraph es b
ásicamente como
NestList, salvo que produce un grafo en vez de una lista. Aplica una funci
ón repetidamente para determinar con cu
áles nodos debe conectarse un nodo particular. En este caso se produce un
árbol de nodos, lo que deja m
ás claro qu
é est
á sucediendo.
Comenzando con
x, se va conectando repetidamente con la lista de nodos obtenidos al aplicar la funci
ón:
Aplicar repetidamente una función numérica para formar otra estructura de árbol:
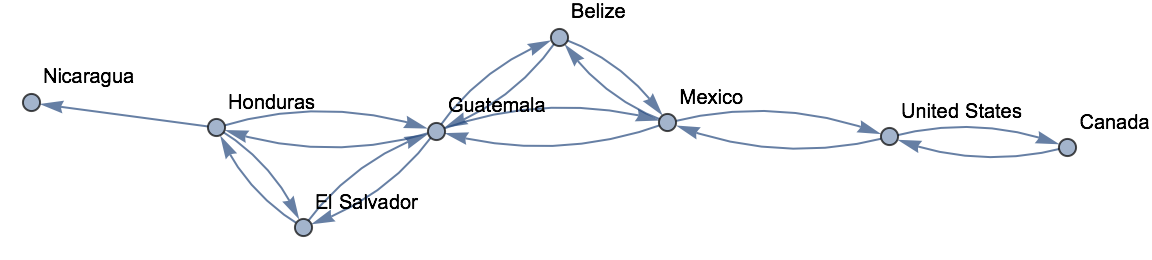
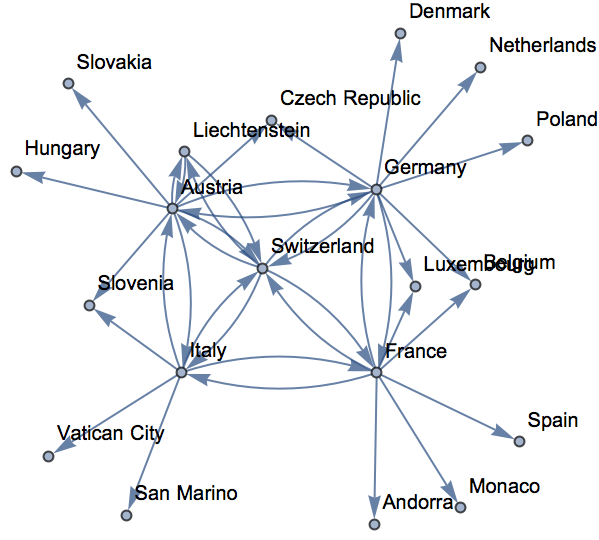
Se puede usar
NestGraph para
“reptar
” hacia afuera, creando una red. Como ejemplo, podr
ía aplicarse repetidamente una funci
ón tal que, para cada pa
ís, produjera la lista de sus pa
íses colindantes. El resultado ser
ía una red que conecta los pa
íses colindantes; as
í, podr
ía comenzarse con Suiza.
“Reptar” hacia afuera 2 pasos a partir de Suiza, conectando cada país con los que le son colindantes:
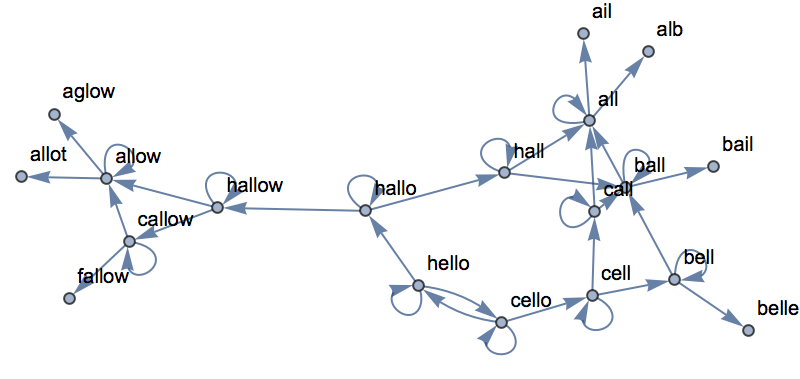
Un ejemplo m
ás: comenzando con la palabra
“hello
”, conecte sucesivamente cada palabra con otras 3 de la lista de palabras comunes que
Nearest considere m
ás cercanas a ella.
Cree una red de palabras cercanas con respecto a cambios de una letra:
| NestList[f,x,n] | | construye la lista que resulte de aplicar f a x hasta n veces |
| Nest[f,x,n] | | obtiene el resultado de aplicar f a x exactamente n veces |
| NestGraph[f,x,n] | | forma un grafo aplicando f con anidación, a partir de x |
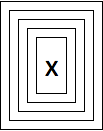
27.1Construya una lista con los resultados de anidar
Blur hasta 10 veces, comenzando con una
“X
” rasterizada de tama
ño 30.
»
27.2Comenzando con
x, forme una lista anidando
Framed hasta 10 veces, con un trasfondo de color aleatorio en cada ocasi
ón.
»
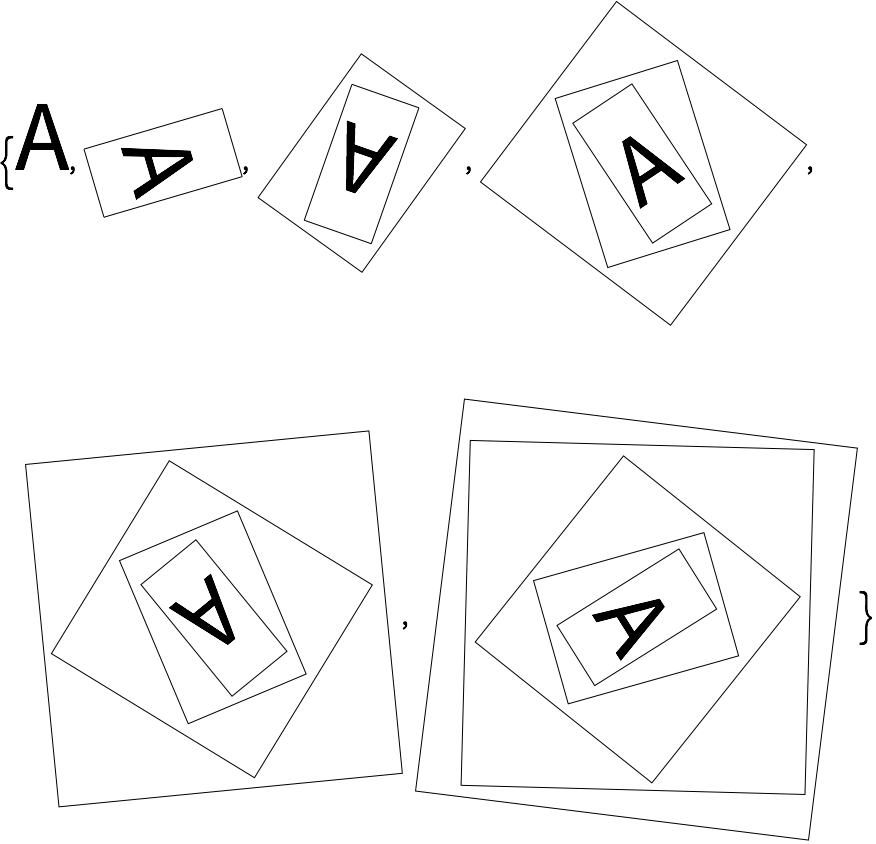
27.3A partir de una
“A
” de tama
ño 50, construya una lista poniendo 5 veces un marco y dando una rotaci
ón aleatoria de manera anidada.
»
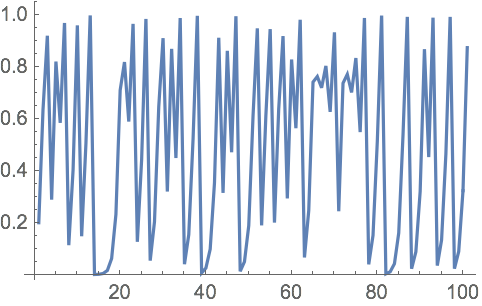
27.4Obtenga un gr
áfico con los puntos unidos de 100 iteraciones del
mapeo logístico 4 #(1-#)&, comenzando en 0.2.
»
27.5Encuentre el valor num
érico del resultado de 30 iteraciones de
1+1/#& comenzando con 1.
»
27.6Cree la lista de las 10 primeras potencias de 3 (comenzando en 0), usando multiplicaci
ón anidada.
»
27.7Forme una lista con los resultados de anidar la funci
ón
(#+2/#)/2& (el
método de Newton) hasta 5 veces, comenzando con 1.0, y restando
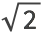
a cada uno de los resultados.
»
27.8Obtenga el gr
áfico, en 2D, de una caminata aleatoria de 1 000 pasos, comenzando en
{0, 0} donde, en cada paso, se a
ñade a las coordenadas una pareja de n
úmeros aleatorios entre
−1 y +1.
»
27.9Obtenga un gr
áfico de arreglo de 50 pasos del tri
ángulo de Pascal m
ódulo 2, comenzando con
{1} y uniendo, de manera anidada,
{0} al principio y al final, y sumando estos resultados m
ódulo 2.
»
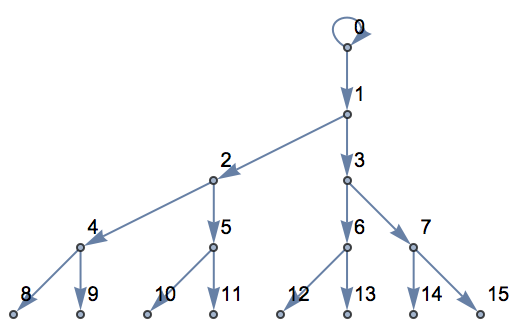
27.10Genere un grafo comenzando de 0, y luego conectando de manera anidada 10 veces cada nodo de valor n con los de valor
n+1 y
2n.
»
27.11Genere un grafo, encontrando de manera anidada los pa
íses colindantes, comenzando con Estados Unidos, durante 4 iteraciones.
»
+27.1Produzca un gr
áfico con los puntos unidos de 100 iteraciones de la
función congruencia lineal Mod[59#, 101]&, comenzando con 1.
»
+27.2Cree la lista de 5
torres de potencias de 2, es decir,
2^2^2...^2 n veces, con n de 0 a 4.
»
+27.3Cree la lista de 20
torres de potencias de 1.2, es decir,
1.2^1.2^...^1.2 n veces, con
n de 0 a 19.
»
+27.4Genere la lista de los valores num
éricos obtenidos en hasta 10 anidaciones de la funci
ón
Sqrt[1+#]&.
»
+27.5Produzca el gr
áfico 3D, de una caminata aleatoria de 1000 pasos, comenzando en
{0, 0, 0} donde, en cada paso, se a
ñade a las coordenadas una terna de n
úmeros aleatorios entre
−1 y +1.
»
¿Cuál es la diferencia entre iteración y recursión?
Si se ejecuta algo repetidamente, se est
á haciendo una iteraci
ón. Si se toma el resultado de una operaci
ón y se le aplica la misma operaci
ón, se trata de una recursi
ón. Se presta un poco a confusi
ón, porque los casos simples de recursi
ón son de iteraci
ón.
NestList siempre efect
úa la recursi
ón, pero si aparece solamente una ranura en la funci
ón, la recursi
ón puede
“desenrollarse
” para convertirse en una iteraci
ón.
¿Qué relación hay entre anidación, recursión y fractales?
Est
án estrechamente relacionados. No hay definiciones precisas, pero los fractales son b
ásicamente formas geom
étricas que exhiben alg
ún tipo de estructura recursiva.
¿Qué es el triángulo de Pascal?
Se trata de una estructura muy com
ún que se describe en las matem
áticas elementales. Su definici
ón es muy cercana al c
ódigo en Wolfram Language que se ha visto aqu
í: en cada fila, cada n
úmero se calcula como la suma de los dos n
úmeros directamente arriba de
él, al lado izquierdo y al derecho. Cada fila contiene los coeficientes del desarrollo de
(1+x)^n.
Conceptualmente, lo es. Se puede concebir como el an
álogo de comenzar en una p
ágina web y visitar, a partir de ah
í, todos los v
ínculos que tiene, y continuar as
í, recursivamente, con el proceso. Se ver
á un ejemplo de esto en la
Sección 44.
¿Cómo es que algunos de los países, pero no todos, tienen flechas bidireccionales en el grafo de países colindantes?
Si se ejecutara
NestGraph en un n
úmero suficiente de pasos, todos los pa
íses tendr
ían flechas bidireccionales; ya que, si A colinda con B, entonces B colinda con A. Pero el proceso se detuvo despu
és del segundo paso, as
í que no se alcanz
ó a llegar a muchas de las conexiones inversas.
No es necesario. Se puede simplemente usar
Power, como en
Table[2^n, {n, 0, 15}]. Pero vale la pena ver c
ómo surge la secuencia
Plus,
Times,
Power del anidamiento sucesivo(p.ej.,
NestList[2+#&, 0, 15] es
Table[2*n, {n, 0, 15}]).
¿Existe alguna forma de detener la aplicación de una función cuando ya no hay cambios en los resultados?
- El ejemplo sobre palabras cercanas puede ser mucho más eficiente calculando, primero, una NearestFunction, y luego usándola repetidamente; mejor que calcular Nearest desde cero para cada palabra. Este ejemplo está estrechamente relacionado con NearestNeighborGraph, que se verá en la Sección 22.

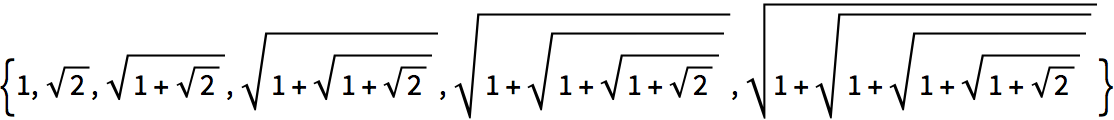
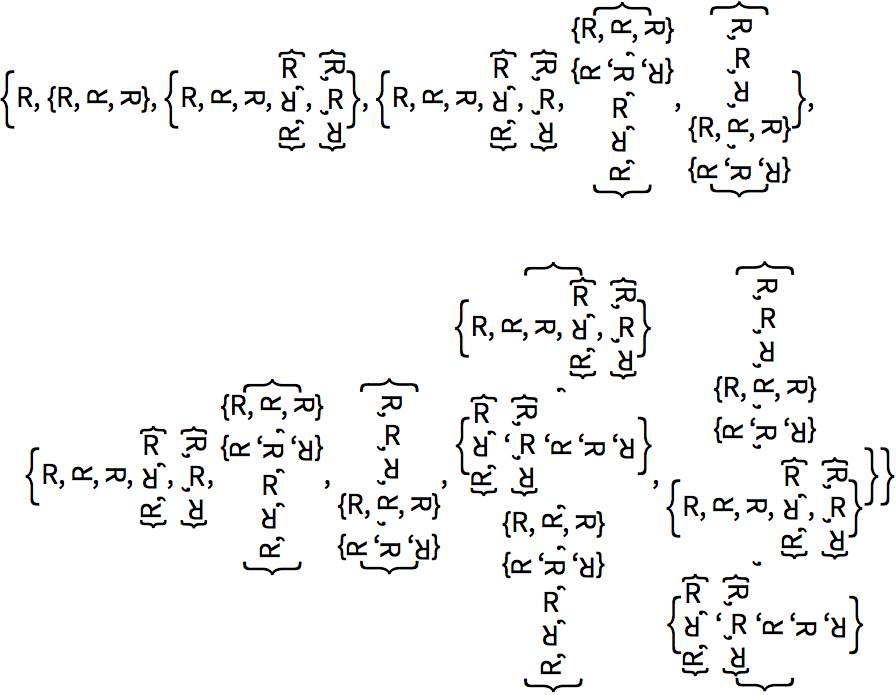

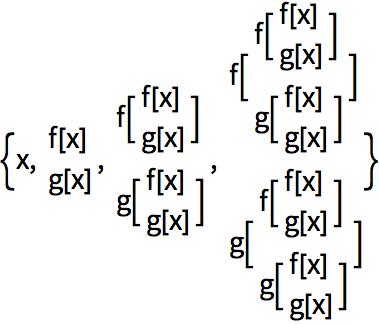
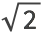 a cada uno de los resultados. »
a cada uno de los resultados. »