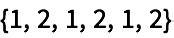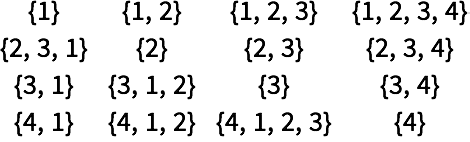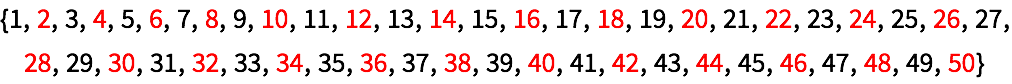| 21 | Grafos y redes |
Un grafo es una forma de mostrar conexiones entre cosas, por ejemplo, cómo están conectadas las páginas web, o cómo se forma una red social entre personas.
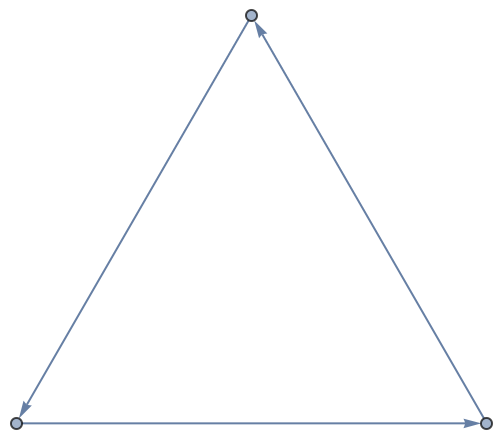
Para comenzar, tomemos un ejemplo sencillo, donde 1 se conecta con 2, 2 con 3 y 3 con 4. Cada conexión se representa mediante (que se escribe en un teclado como ->).
Un grafo de conexiones muy sencillo:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= | 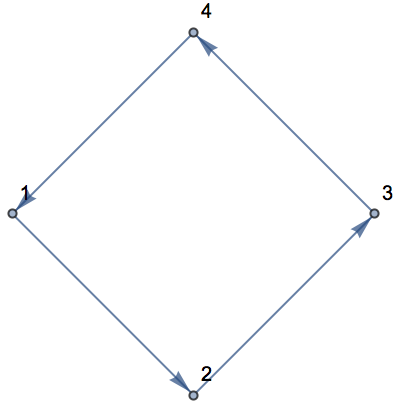
|
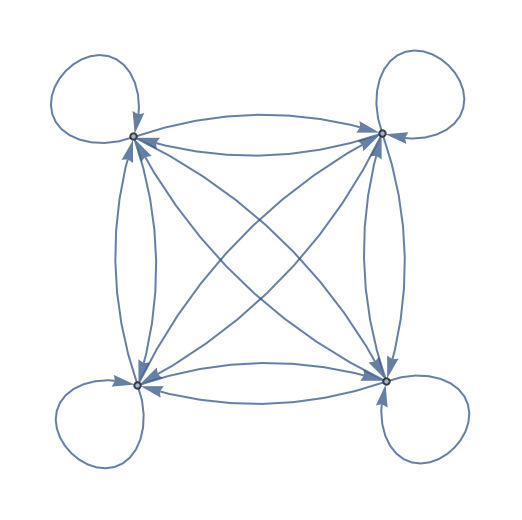
Se añaden dos conexiones más, incluyendo una que conecta el 2 consigo mismo:
| In[4]:= |
| Out[4]= | 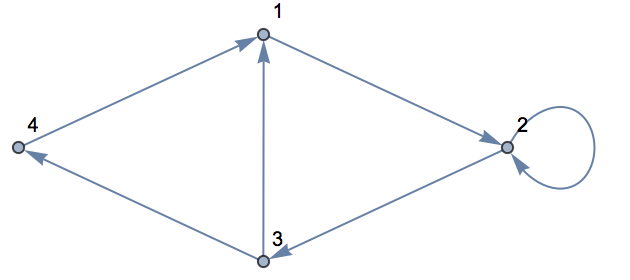
|
A medida que se añaden conexiones, Wolfram Language escoge maneras diferentes de colocar los vértices o nodos del grafo. Sin embargo, lo que realmente importa para su significado, es cómo están conectados los vértices. Si no se especifica otra cosa, Wolfram Language tratará de acomodar las cosas de tal modo que queden lo menos enredadas y más fáciles de entender que sea posible.
Pero hay opciones para especificar otras formas de disponer las cosas. Por ejemplo, aquí se tiene el mismo grafo anterior, con las mismas conexiones, pero la disposición de los vértices es diferente.
| In[5]:= |
| Out[5]= | 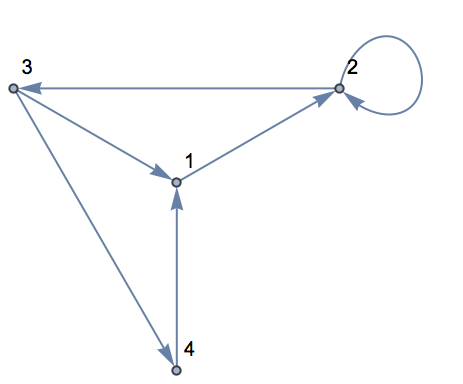
|
Se pueden hacer procesos de cómputo en el grafo, tal como, por ejemplo, encontrar el camino más corto que vaya de 4 a 2, siempre en la dirección de las flechas.
El camino más corto de 4 a 2 en el grafo pasa por 1:
| In[6]:= |
| Out[6]= |
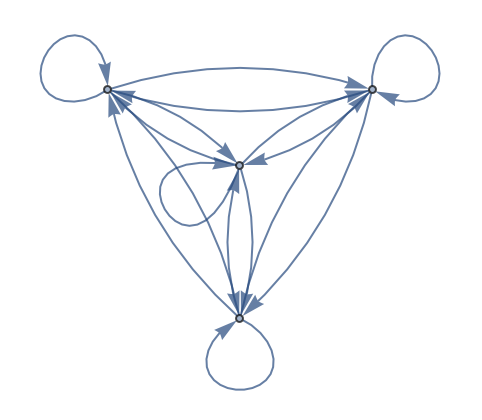
Considere otro grafo. Ahora se tienen 3 nodos, con conexión entre cada uno de ellos.
Primero, se crea un arreglo con todas las conexiones posibles entre 3 objetos:
| In[7]:= |
| Out[7]= |
Aquí el resultado es una lista de listas, y lo que requiere Graph es una sola lista con las conexiones. Y esto se puede obtener usando Flatten para “aplanar” las sublistas.
| In[8]:= |
| Out[8]= |
Del arreglo, se obtiene una lista “aplanada” de las conexiones:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 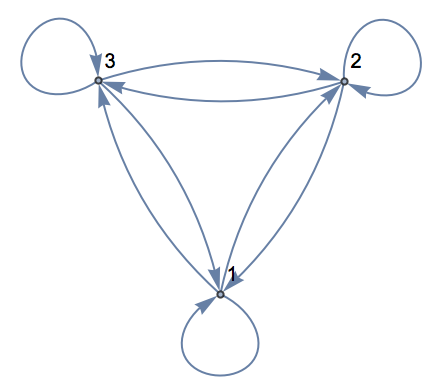
|
| In[11]:= |
| Out[11]= | 
|
| In[12]:= |
| Out[12]= | 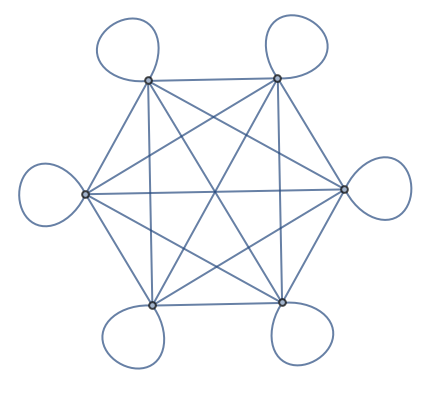
|
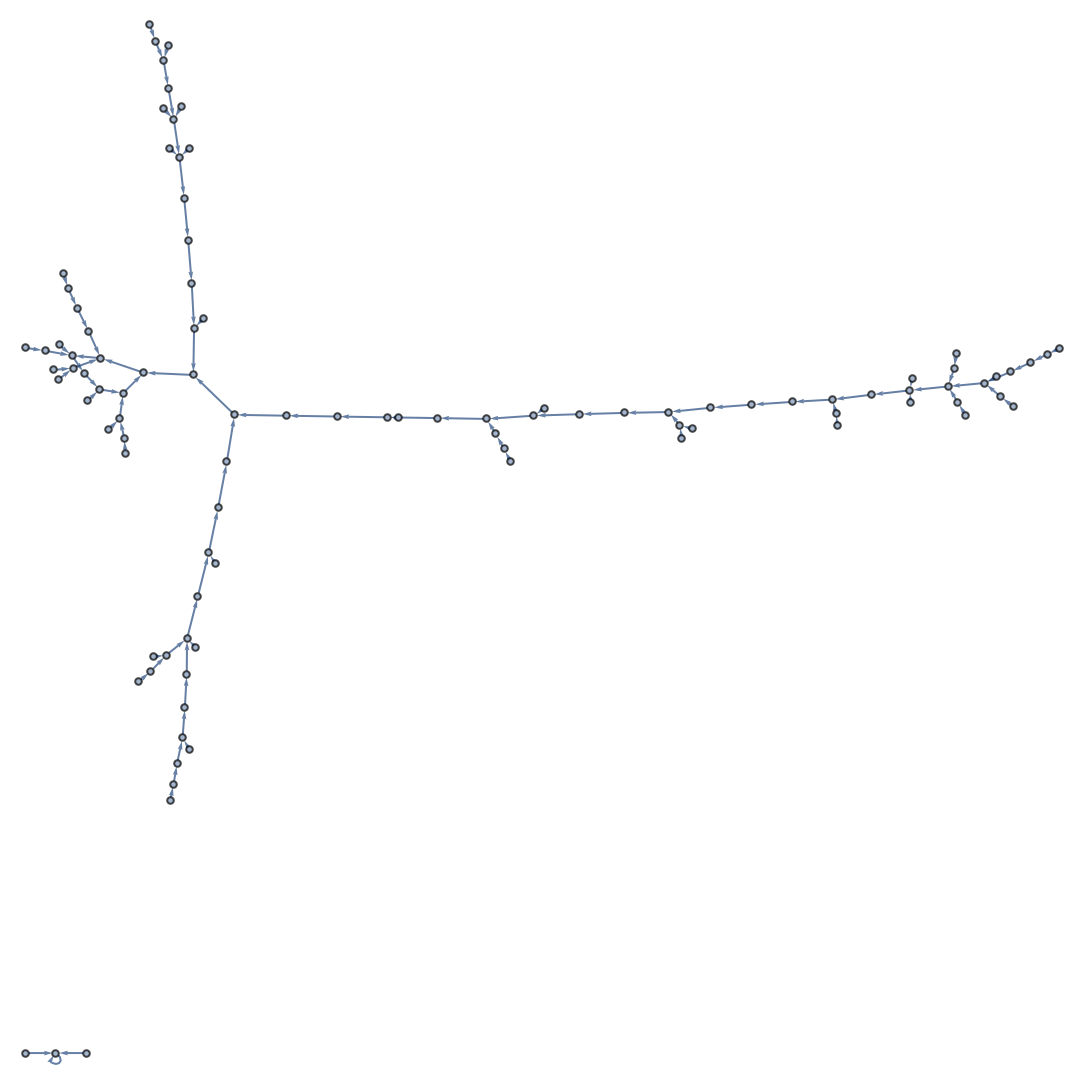
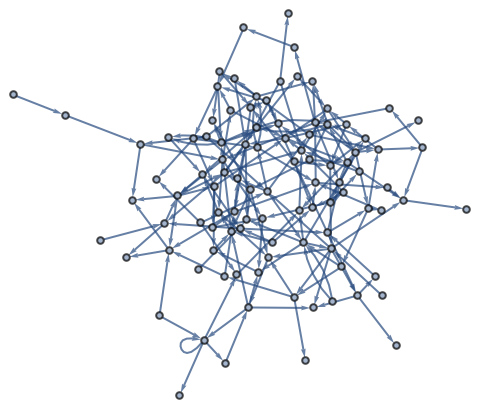
Ahora se construye un grafo con conexiones aleatorias. He aquí un ejemplo con 20 conexiones entre nodos elegidos al azar.
Construya un grafo con 20 conexiones entre nodos elegidos al azar y numerados del 0 al 10:
| In[13]:= |
| Out[13]= | 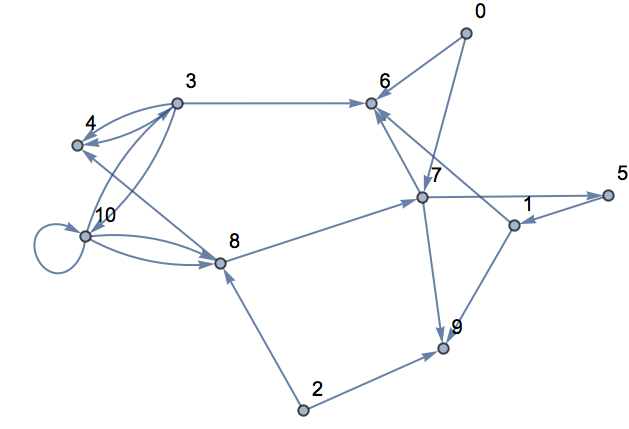
|
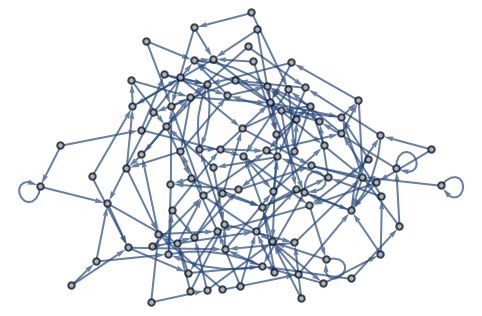
Se obtendrá un grafo diferente si se generan diferentes números al azar. He aquí 6 grafos.
Seis grafos generados aleatoriamente son:
| In[14]:= |
| Out[14]= | 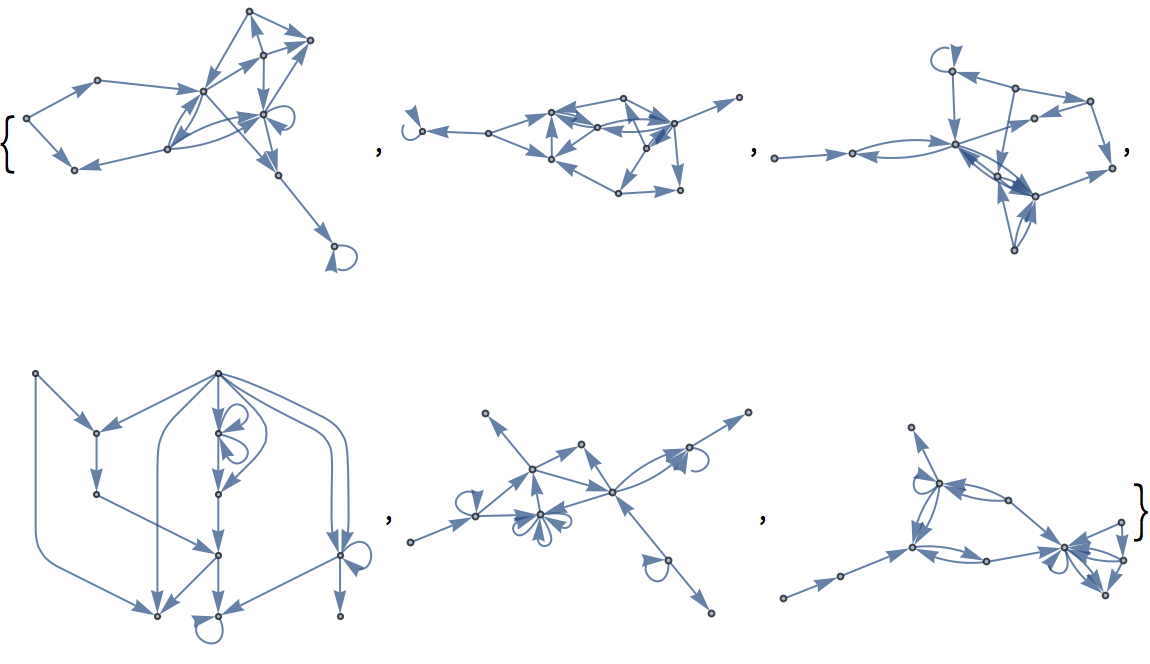
|
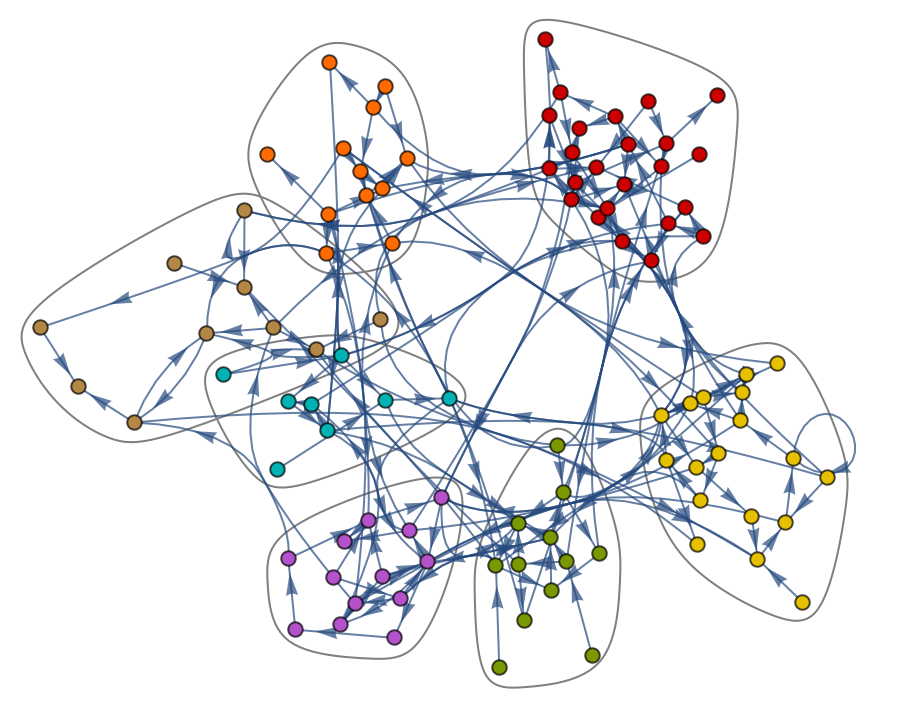
Hay muchos análisis que pueden llevarse a cabo con los grafos. Por ejemplo, se puede descomponer un grafo en “comunidades”, es decir, en grupos de nodos que están más conectados entre ellos que con el resto del grafo. Se hará ahora esto con un grafo aleatorio.
| In[15]:= | 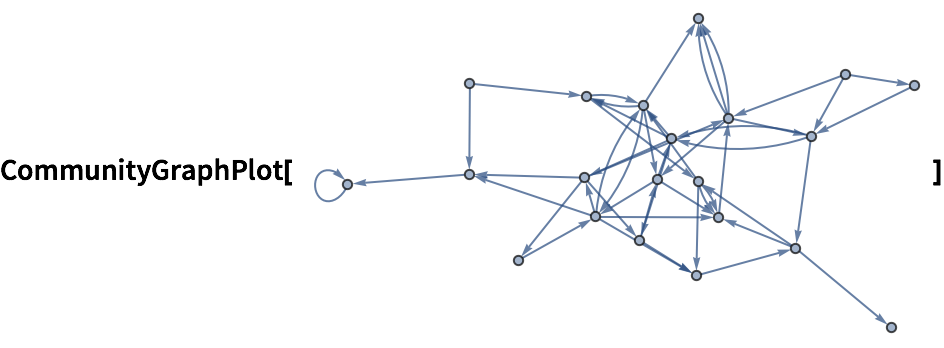
|
| Out[15]= | 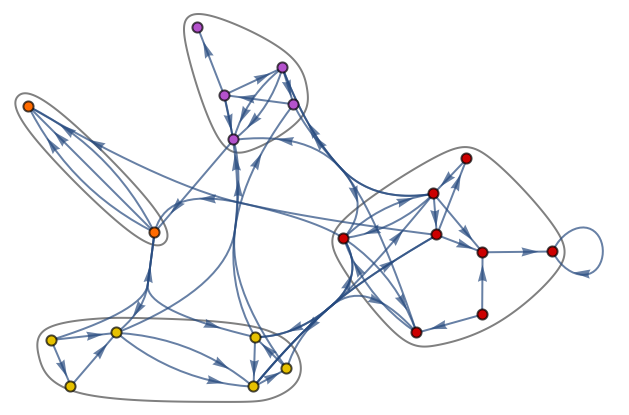
|
El resultado es un grafo con exactamente las mismas conexiones que el original, pero con los nodos acomodados de manera que se ilustre la “estructura de comunidades” del grafo.
| Graph[{ij, ...}] | un grafo o red de conexiones | |
| UndirectedGraph[{ij, ...}] | un grafo sin direcciones en las conexiones | |
| VertexLabels | una opción para especificar etiquetas de vértices (e.g. All) | |
| FindShortestPath[graph,a,b] | encuentra el camino más corto entre un nodo y otro | |
| CommunityGraphPlot[list] | presenta un grafo de modo tal que muestre las “comunidades” | |
| Flatten[list] | aplana las sublistas de una lista |
21.1Construya un grafo consistente en un bucle de tres nodos. »
21.3Construya una tabla de grafos no dirigidos con entre 2 y 10 nodos, donde todos los nodos estén conectados. »
21.5Muestre una gráfica con puntos unidos del resultado de concatenar todos los dígitos de los enteros del 1 al 100 (i.e. ..., 8, 9, 1, 0, 1, 1, 1, 2, ...). »
21.8Presente un grafo donde cada conexión conecte i con j-i, donde tanto i como j varíen de 1 a 5. »
21.9Genere un grafo con 100 nodos, donde cada uno conecte con otro escogido al azar. »
21.10Genere un grafo con 100 nodos, donde cada nodo conecte con dos nodos escogidos al azar. »
21.11Para el grafo {12, 23, 34, 41, 31, 22}, forme un arreglo donde aparezcan los caminos más cortos entre cada par de nodos, de modo que el nodo inicial marque la fila del arreglo y el final marque la columna. »
+21.1Presente un grafo con 4 nodos donde todos los nodos estén conectados, mostrando el resultado en un dibujo radial. »
+21.3Use Flatten para generar una tabla de los números 1 al 50, donde los pares estén en color rojo. »
+21.4Use ImageData, Flatten y Total para encontrar el número de píxeles en blanco de Binarize[Rasterize["W"]]. »
+21.5Use Flatten, IntegerDigits y Total para encontrar la suma de todos los dígitos de los números enteros hasta el 1000. »
+21.6Genere un grafo con 200 conexiones, cada una entre nodos cuyos números se elijan al azar entre 0 y 100. »
+21.7Genere una gráfica que muestre las comunidades en un grafo aleatorio con nodos numerados del 0 al 100, y que tenga 200 conexiones. »
¿Qué diferencia hay entre un “grafo” y una “red”?
No hay diferencia. Son simplemente palabras diferentes para la misma cosa, aunque “grafo” suele usarse más en matemáticas, mientras que “red” es más común en otras áreas más aplicadas.
En un grafo, los vértices son sus puntos o nodos. Las aristas son las conexiones. Los grafos han surgido en tantos campos diferentes que existe una amplia variedad de nombres para la misma cosa.
Significa Rule[i, j]. Las reglas se usan en muchas partes de Wolfram Language, tales como la especificación de opciones.
Sí. Use SocialMediaData["Facebook", "FriendNetwork"]. Note que solamente estarán incluidos los amigos que así se hayan manifestado en Facebook. (Vea la Sección 44).
¿De qué tamaño puede ser un grafo en Wolfram Language?
La limitación principal es la cantidad de memoria de la computadora que se use. Grafos con decenas o centenares de miles de nodos no plantean ningún problema.
¿Se pueden especificar propiedades para nodos y aristas?
Sí. Pueden proporcionarse a Graph listas de nodos y aristas que incluyan cosas tales como Property[nodo, VertexStyleRed] o Property[arista, EdgeWeight20]. Pueden darse también opciones globales a Graph.
- Los grafos, al igual que las cadenas de caracteres, imágenes, gráficas, etc., son objetos de primera clase en Wolfram Language.
- Se pueden ingresar aristas no dirigidas en un grafo usando <->, que aparece como .
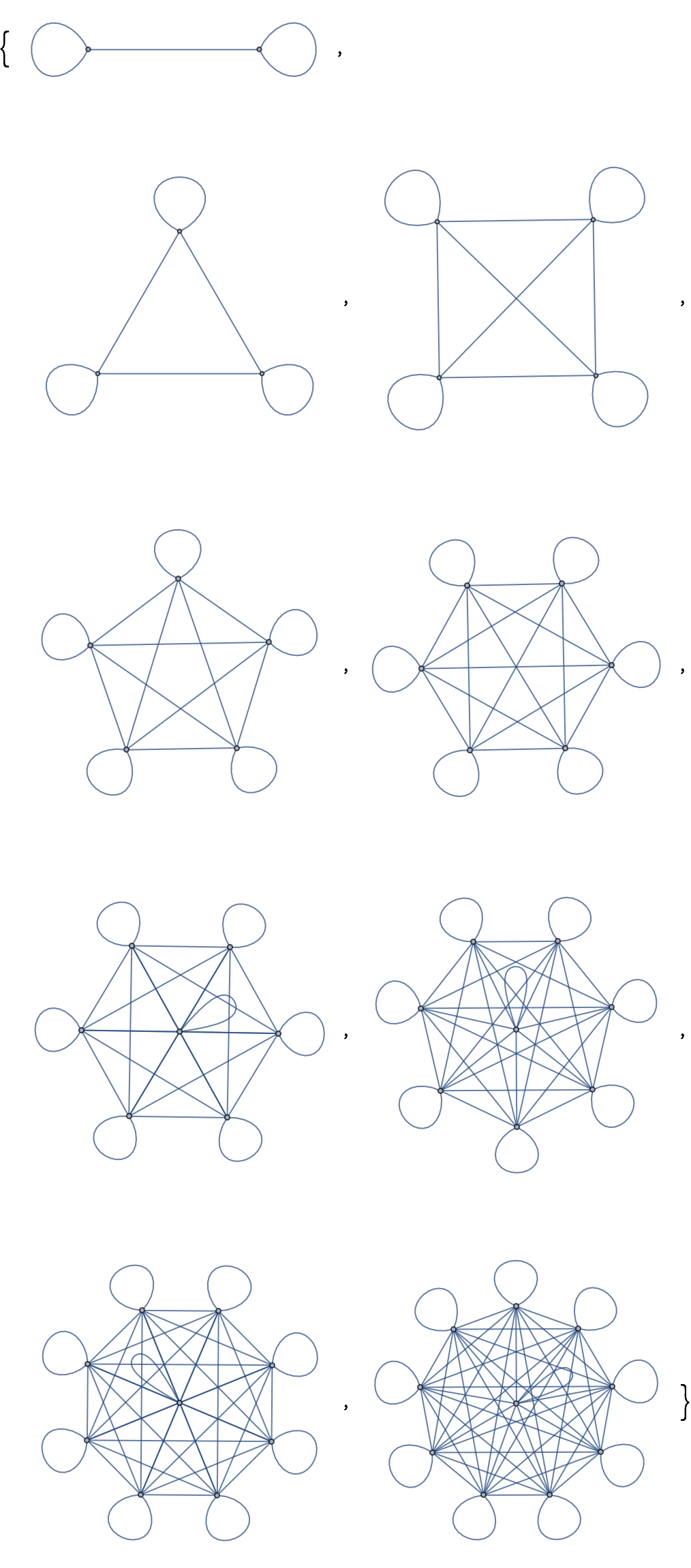
- CompleteGraph[n] da el grafo completamente conexo con n nodos. Entre otros tipos de grafos especiales se encuentran KaryTree, ButterflyGraph, HypercubeGraph, etc.
- Hay muchas maneras de construir grafos aleatorios (conexiones aleatorias, números aleatorios de conexiones, redes libres de escala, etc.). RandomGraph[{100, 200}] produce un grafo aleatorio con 100 nodos y 200 aristas.
- AdjacencyMatrix[grafo] da la matriz de adyacencia de un grafo. AdjacencyGraph[matriz] construye un grafo a partir de una matriz de adyacencia.
- PlanarGraph[grafo] intenta rearreglar un grafo de tal manera que no haya cruzamientos de aristas, si así fuera posible.