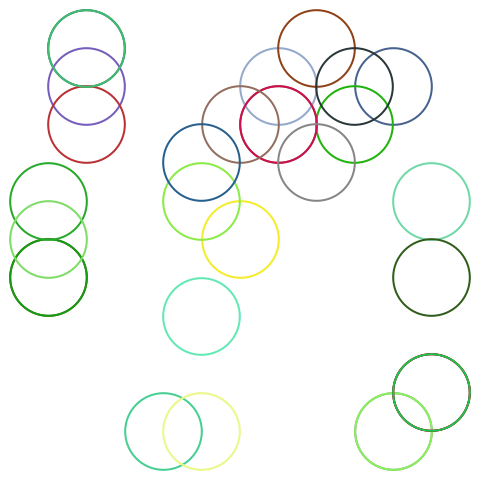An Elementary Introduction to the Wolfram Language
14Coordenadas y gráficos
ListPlot y ListLinePlot se han venido usando para obtener los gráficos de listas de valores dados en forma consecutiva. Si se consideran listas compuestas de parejas de coordenadas, en vez de valores individuales, aquellas funciones podrán usarse para obtener los gráficos de puntos que estén en posiciones arbitrarias.
Represente gráficamente una lista de valores donde cada uno de ellos aparece después del anterior:
In[1]:=
Click for copyable input
Out[1]=
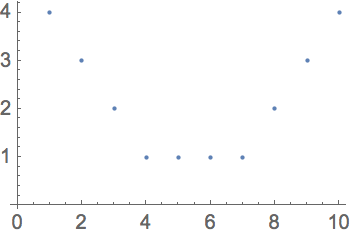
Represente gráficamente una secuencia de puntos arbitrarios, especificados por sus coordenadas {x, y}:
In[2]:=
Click for copyable input
Out[2]=
Aquí la posición de cada punto está especificada por sus coordenadas {x, y}. De acuerdo con el uso convencional en matemáticas, el valor x indica hasta qué distancia se encuentra el punto en la dirección horizontal, mientras que el valor y indica hasta qué distancia está en la dirección vertical.
Genere una secuencia de coordenadas {x, y} aleatorias:
In[3]:=
Click for copyable input
Out[3]=
Otra forma de obtener coordenadas aleatorias es:
In[4]:=
Click for copyable input
Out[4]=
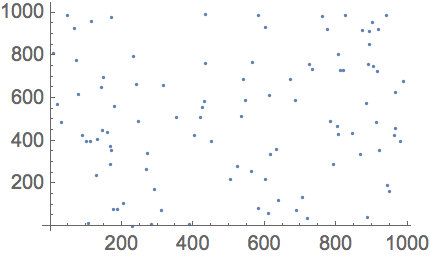
Represente gráficamente 100 puntos con coordenadas aleatorias:
In[5]:=
Click for copyable input
Out[5]=
Las coordenadas pueden usarse para construir gráficos. Anteriormente se vio cómo graficar un círculo. Para hacer gráficos de más de un círculo hay que indicar dónde queda cada uno, lo que se consigue dando las coordenadas de sus centros.
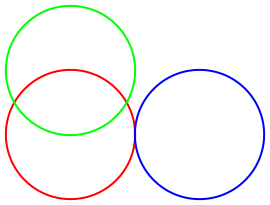
Sitúe varios círculos, dando las coordenadas de sus centros:
In[6]:=
Click for copyable input
Out[6]=
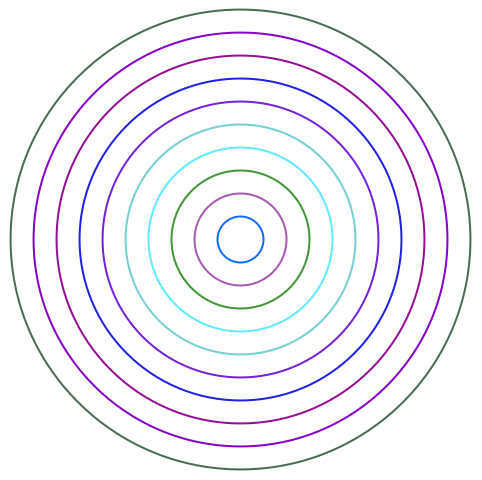
Es más fácil distinguir cada uno de los círculos cuando se aplican estilos de color:
In[7]:=
Click for copyable input
Out[7]=
Presente gráficamente 100 círculos colocados al azar, donde las coordenadas de los centros estén entre 0 y 50:
In[8]:=
Click for copyable input
Out[8]=
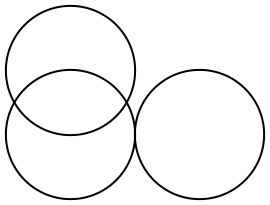
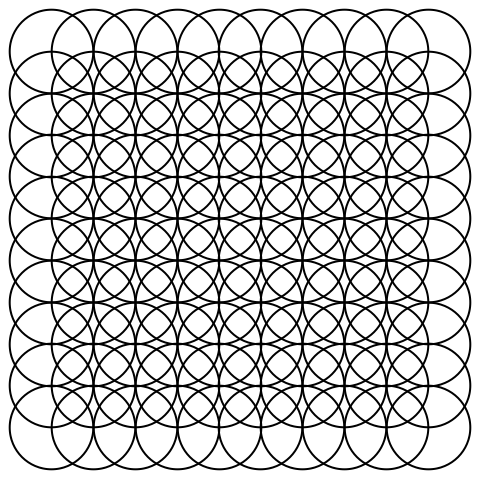
Un arreglo de círculos en 2D, acomodados de manera que apenas se toquen uno con otro:
In[9]:=
Click for copyable input
Out[9]=
Circle[{x,y}] quiere decir un círculo con centro en la posición {x,y}, y si no se dice otra cosa, ese círculo tiene radio 1. Pero puede hacerse un círculo de radio cualquiera usando Circle[{x,y},r].
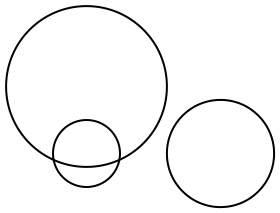
Use radios diferentes para círculos diferentes:
In[10]:=
Click for copyable input
Out[10]=
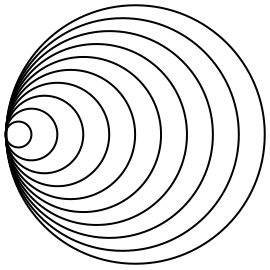
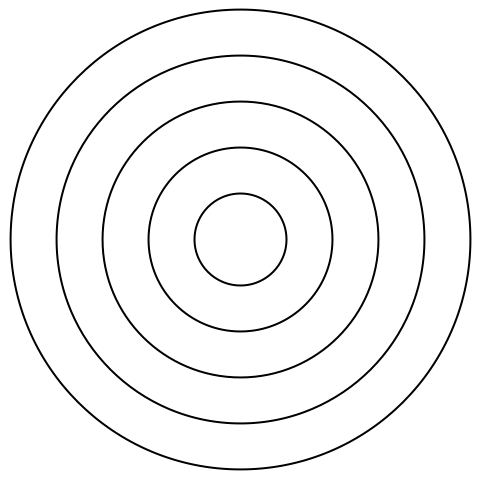
Cree 10 círculos concéntricos:
In[11]:=
Click for copyable input
Out[11]=
Dibuje círculos cada vez más grandes cuyos centros se vayan corriendo progresivamente hacia la derecha:
In[12]:=
Click for copyable input
Out[12]=
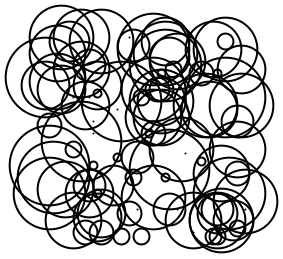
Escoja al azar tanto las posiciones como los radios:
In[13]:=
Click for copyable input
Out[13]=
RegularPolygon funciona de manera muy parecida a Circle y Disk, salvo que, además de dar la posición del centro y el tamaño, hay que indicar de cuántos lados es el polígono.
Presente gráficamente un pentágono regular de tamaño 1 y un heptágono regular de tamaño 0.5:
In[14]:=
Click for copyable input
Out[14]=
Pueden mezclarse diferentes clases de objetos gráficos:
In[15]:=
Click for copyable input
Out[15]=
Para producir gráficos arbitrarios es necesario utilizar las primitivas gráficas básicas Point, Line y Polygon. Point[{x,y}] representa un punto en la posición de coordenadas {x,y}. Para obtener varios puntos se puede dar una lista de Point[{x,y}]s, o bien una lista de coordenadas de posición dentro de un único Point.
Presentación gráfica de tres puntos en posiciones especificadas:
In[16]:=
Click for copyable input
Out[16]=
La forma alternativa es reunir todas las coordenadas de posición en una sola lista:
In[17]:=
Click for copyable input
Out[17]=
Dibuje una línea que una las posiciones:
In[18]:=
Click for copyable input
Out[18]=
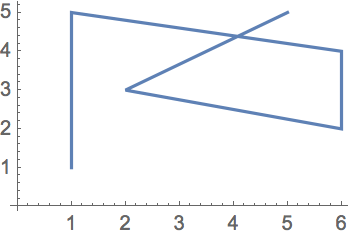
Haga un polígono cuyas esquinas estén en las posiciones que se indiquen:
In[19]:=
Click for copyable input
Out[19]=
RegularPolygon construye un polígono en que todos los lados y los ángulos son iguales. Polygon hace un polígono cualquiera, aun si se quiere que se doble sobre sí mismo, por extraño que parezca.
Un polígono de 20 esquinas en posiciones aleatorias entre 0 y 100; este polígono se dobla sobre sí mismo:
In[20]:=
Click for copyable input
Out[20]=
Lo que se ha hecho hasta ahora puede generalizarse a 3D. En vez de dos coordenadas {x, y} ahora se usan tres: {x, y, z}. En Wolfram Language, la x aumenta hacia la derecha a través de la pantalla, la y se “mete dentro” de la pantalla, y la z aumenta de abajo hacia arriba.
Dos esferas apiladas, una encima de la otra:
In[21]:=
Click for copyable input
Out[21]=
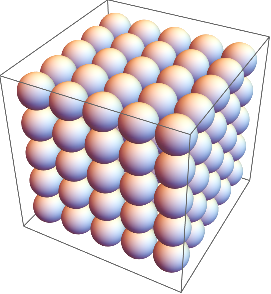
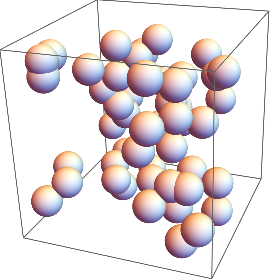
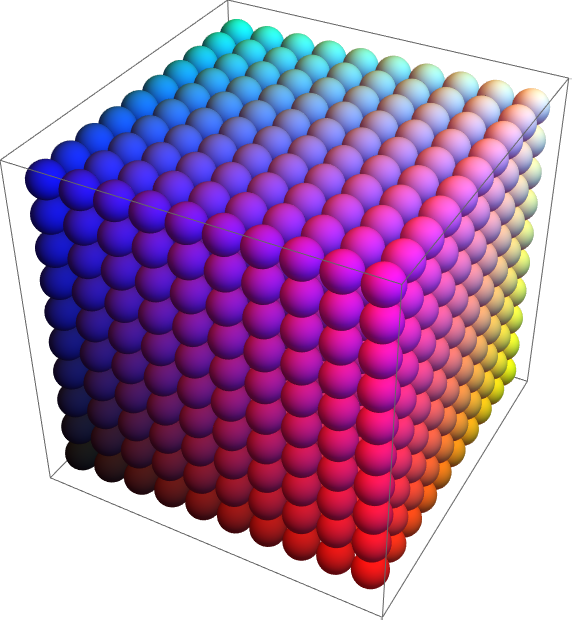
Un arreglo en 3D de esferas (un radio común de 1/2 hace que apenas se toquen):
In[22]:=
Click for copyable input
Out[22]=
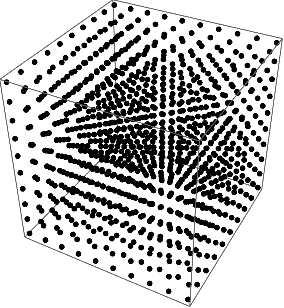
Un arreglo de puntos en 3D:
In[23]:=
Click for copyable input
Out[23]=
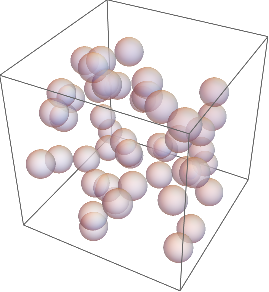
50 esferas con posiciones aleatorias en 3D, donde cada coordenada varía entre 0 y 50:
In[24]:=
Click for copyable input
Out[24]=
Los objetos en 3D aparecen como sólidos, a menos que se indique otra cosa, de tal manera que no puede verse a través de ellos. Pero así como puede especificarse el color de algo, también puede especificarse su opacidad. Opacidad 1 significa completamente opaco, de modo que no puede verse nada a través del objeto; opacidad 0 quiere decir completamente transparente.
Especifique una opacidad de 0.5 para todas las esferas:
In[25]:=
Click for copyable input
Out[25]=
El uso de Manipulate permite la manipulación de objetos gráficos en 2D o en 3D.
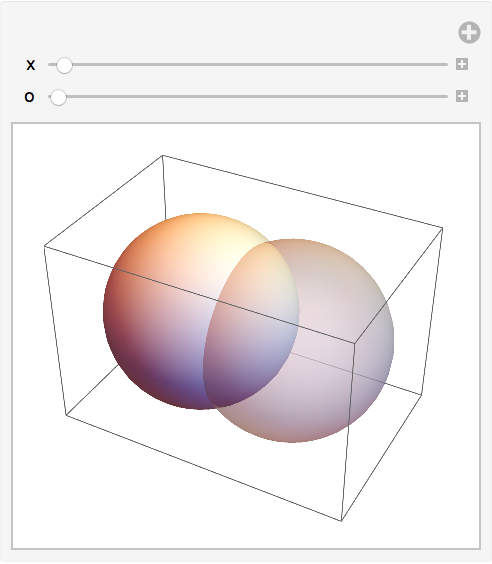
Manipule la posición y la opacidad de la segunda esfera:
In[26]:=
Click for copyable input
Out[26]=
Vocabulario
Point[{x,y}] un punto con coordenadas {x, y}
Line[{{1,1},{2,4},{1,2}}] una recta que conecta las coordenadas especificadas
Circle[{x,y}] un círculo con centro en {x, y}
Circle[{x,y},r] un círculo con centro en {x, y} y de radio r
RegularPolygon[{x,y},s,n] un polígono regular con centro {x, y}
y n lados, cada uno de longitud s
Polygon[{{1,1},{2,4},{1,2}}] un polígono con las esquinas especificadas
Sphere[{x,y,z}] una esfera con centro en {x, y, z}
Sphere[{x,y,z},r] una esfera con centro en {x, y, z} y de radio r
Opacity[level] especifica un nivel de opacidad (0: transparente; 1: sólido)
14.1Presente gráficamente 5 círculos concéntricos centrados en {0, 0} con radios 1, 2, ... , 5. »
Salida esperada:
Out[]=
14.2Cree 10 círculos concéntricos con colores aleatorios. »
Muestra de salida esperada:
Out[]=
14.3Presente gráficamente una cuadrícula de 10×10 círculos de radio 1 en los puntos de coordenadas enteras {x, y}. »
Salida esperada:
Out[]=
14.4Forme una cuadrícula de 10×10 puntos cuyas coordenadas sean enteras en las posiciones del 1 al 10. »
Salida esperada:
Out[]=
14.5Escriba un Manipulate con entre 1 y 20 círculos concéntricos. »
Muestra de salida esperada:
Out[]=
14.6Coloque 50 esferas, de colores aleatorios, en coordenadas enteras aleatorias entre 0 y 10. »
Muestra de salida esperada:
Out[]=
Salida esperada:
Out[]=
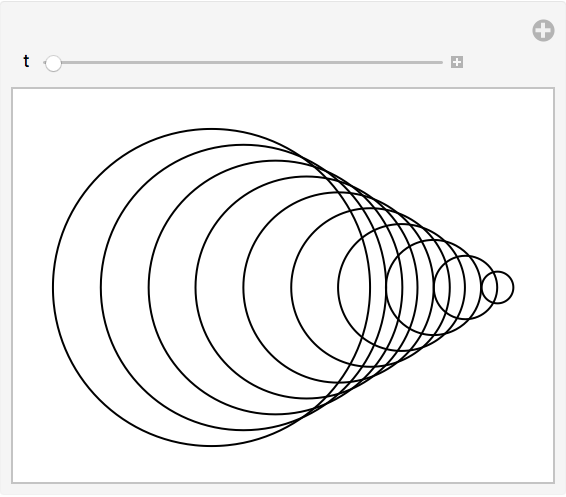
14.8Formule un Manipulate que contenga círculos de radio x, centrados en {t*x, 0}, donde t varíe entre −2 y +2, y tal que x varíe entre 1 y 10. »
Muestra de salida esperada:
Out[]=
14.9Forme un arreglo de 5×5 hexágonos regulares con lados de 1/2 y centrados en puntos enteros. »
Salida esperada:
Out[]=
Muestra de salida esperada:
Out[]=
+14.1Establezca un Manipulate para crear una cuadrícula regular de n×n puntos en posiciones enteras, donde n varíe de 5 a 20. »
Muestra de salida esperada:
Out[]=
+14.2Coloque 30 círculos de radio 1, con colores aleatorios, en coordenadas enteras al azar, entre 0 y 10. »
Muestra de salida esperada:
Out[]=
+14.3Muestre 100 polÍgonos con tamaños de lado aleatorios entre 3 y 8, con opacidad de .5 y colores aleatorios y con coordenadas aleatorias enteras entre 0 y 100. »
Muestra de salida esperada:
Out[]=
+14.4Haga un arreglo de 10×10×10 puntos en 3D, donde cada punto tenga un color diferente. »
Muestra de salida esperada:
Out[]=
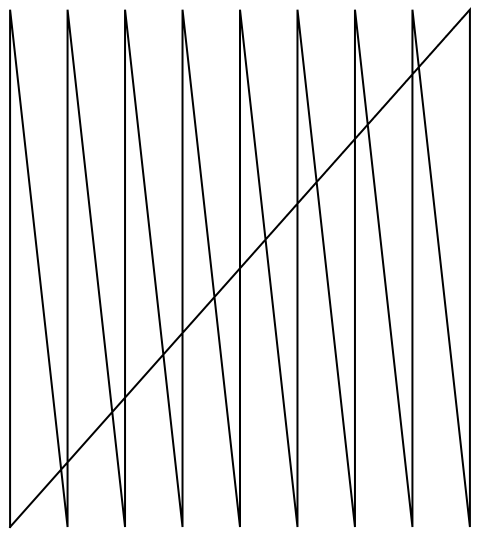
+14.5Tome los dos primeros dígitos de los números del 10 al 100 y trazar una línea que los tenga como coordenadas. »
Salida esperada:
Out[]=
+14.6Tome los 3 primeros dígitos de los números entre 100 y 1000 y dibujar una línea en 3D que los use como coordenadas. »
Salida esperada:
Out[]=
Preguntas y respuestas
¿Qué es lo que determina la amplitud de las coordenadas que se muestran?
Por defecto, se selecciona automáticamente, pero se puede fijar explícitamente usando la opción PlotRange, como se explica en la Sección 20.
¿Cómo pueden colocarse ejes en los gráficos?
Usando la opción AxesTrue (ver la Sección 20) .
¿Cómo puede cambiarse la apariencia de los bordes de un polígono o disco?
Usando EdgeForm dentro de Style.
¿Cuáles otras construcciones hay?
Hay bastantes. Algunos ejemplos son Text (para colocar texto dentro de un gráfico), Arrow (para colocar puntas de flecha en líneas, etc.), Inset (para poner gráficos dentro de otros gráficos) y FilledCurve.
¿Cómo se quita la caja alrededor de las gráficos 3D?
Usando la opción BoxedFalse (ver la Sección 20) .
Notas técnicas
Paea explorar más
Guía para Graphics en Wolfram Language »
 
Download Notebook Version
en