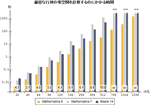
Mathematica 8のコアとなるアルゴリズムには，記号的あるいは数値的に方程式および不等式を大域的に解くための新世代メソッド等の多数の劇的な向上点が加わっている．新しい記号・数値メソッドにより，高度に振動する広範な関数のクラスを自動的に数値積分することができる．Mathematica 8は厳密な線形代数のパフォーマンスにおいて最高レベルに到達しており，世界最大の特殊関数コレクションに多数の関数が追加されている．

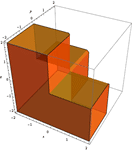
• Solveで複素数，実数，整数領域の方程式および不等式を解くことができる »
• NSolveで複素数および実数領域の方程式・不等式を解くことができる »
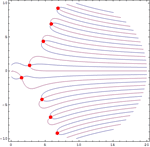
• SolveおよびNSolveに，超越方程式を解くための新しい高度なメソッドが加わった
• SolveおよびNSolveに，高次多項式の実数解を見付けるための新しい高度なメソッドが加わった
• 偏関数を表すための条件付きで有効な式が新しく加わった »
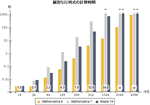
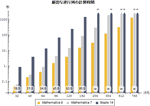
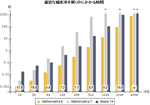
• 新世代の高速かつ厳密な線形代数 »
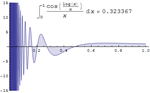
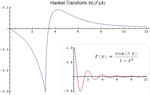
• 高度に振動する関数を積分するための，記号・数値の新しいハイブリッドメソッド »
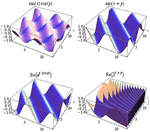
• 確率および統計用の新しい特殊関数 »

条件付きで有効な解を使って計算する »	連立方程式のパラメータ化された実数解を見付ける »	超越方程式を数値的に解く »
高次の実整方程式を数値的に解く »	条件付きで有効な式 »	整数行列に対する行列式の高速計算 »
整数行列に対する逆行列の高速計算 »	整数係数を持つ連立線形方程式を素早く解く »	整数行列に対する零空間の高速計算 »
数値積分のチャレンジ問題を解く »	振動関数の和，積，合成を積分する »	高度に振動する多次元関数を積分する »
多角形上の二変量正規分布の確率を求める »	RankedMinの部分レベル集合 »	ラプラス方程式の固有関数 »
高階の導関数の値を直接計算する »	数値的なハンケル変換を実行する »

関連関数

Solve  NSolve  ConditionalExpression  NIntegrate  LinearSolve  NullSpace  MatrixRank  Inverse  LeastSquares  PseudoInverse  Det  Dot  MarcumQ  OwenT  WignerD  BellY  RankedMin  RankedMax