核心算法
新增和改进的核心算法
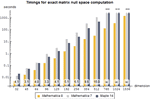
Mathematica 8 对其核心算法进行了大量显著的改进,其中包括对方程组和不等式进行数值式或符号式全局求解的新一代方法。新的符号数值方法使您可以以数值方式对多种类型的高度振荡的函数自动求 积分。Mathematica 8 在精确线性代数性能上达到一个新的水准,而且具有世界上最大集合的特殊函数。
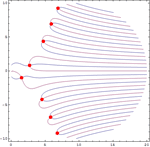
- Solve 可以求解包含复数、实数和整数的方程组和不等式。 »
- NSolve 可以求解包含复数和实数的方程组和不等式。 »
- Solve 和 NSolve 提供了求解超越方程的高级方法。
- Solve 和 NSolve 提供了求高次多项式的实解的高级方法。
- 新的有效条件表达式用于表示部分函数。 »
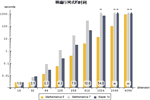
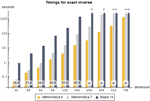
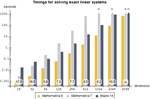
- 快速精确地进行线性代数运算的新一代方法。 »
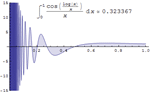
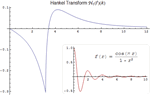
- 新的用于积分高振荡函数的混合符号数值方法。 »
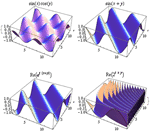
- 新的用于概率和统计的特殊函数。 »