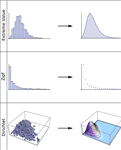
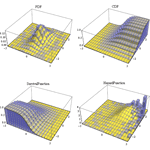
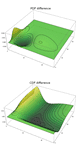
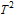核心算法
参数估计和检验
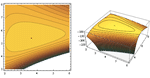
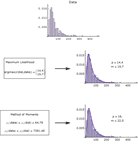
利用 Mathematica 完美地集成的符号和数值功能,Mathematica 8 为100多个内置参数分布和导出分布构建器提供高度自动和有效的参数估计和拟合优度检验。求解器和优化程序的自动选择使用户可以把注意力集中在他们想要解决的问题,而不用担心算法细节,可选设置使您在必要时对最优化和具体假设检验进行完全控制。只需几行简短的代码就可以进行估计和检验,让研究人员、分析师、教师或学生能够快速进入决策和工作报告阶段。
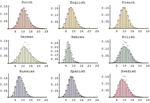
- 适用于所有参数和导出分布的高度自动的参数估计。 »
- 最大似然和基于矩的参数估计。 »
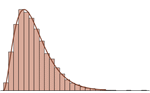
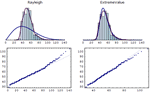
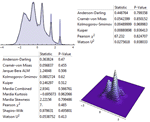
- 单变量、多变量、离散和连续数据的拟合优度测试。 »
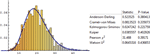
- 直接访问 Kolmogorov-Smirnov、Pearson
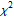 、Anderson-Darling 检验等。 »
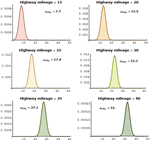
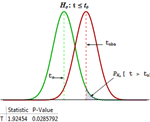
、Anderson-Darling 检验等。 » - 对任意数量的数据集的自动定位和尺度假设检验。 »
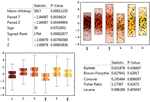
- 全套已命名的定位和度量检验,包括
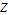 、
、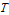 、符号、Levene 等。 »
、符号、Levene 等。 » - 检验结果的完全集合,包括检验统计量、
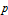 值、报告等。 »
值、报告等。 »