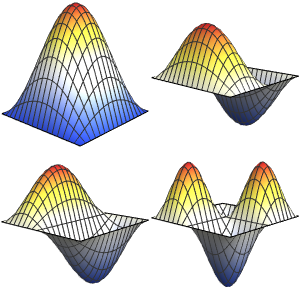
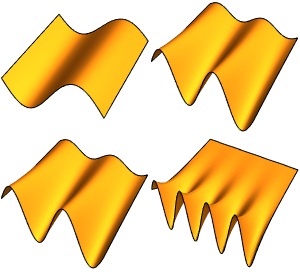
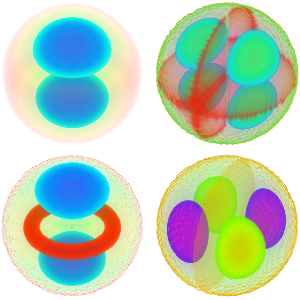
拉普拉斯算子的本征值和本征函数
在一个一维区域上求解拉普拉斯算子最小的四个特征值和特征函数, 即 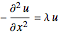 的解.
的解.
设定拉普拉斯算子.
In[1]:=
\[ScriptCapitalL] = -Laplacian[u[x], {x}];用数值方法求最小的四个特征值和特征函数.
In[2]:=
NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4]Out[2]=

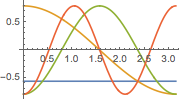
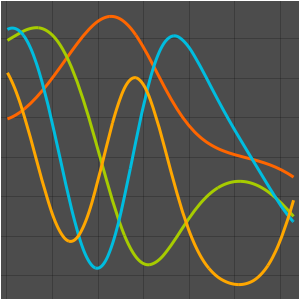
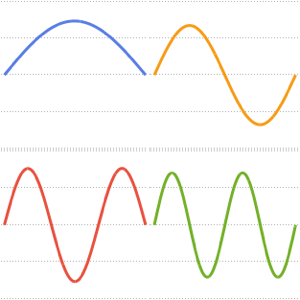
可视化特征函数.
In[3]:=
NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4];
Plot[Evaluate[%[[2]]], {x, 0, \[Pi]}]Out[3]=