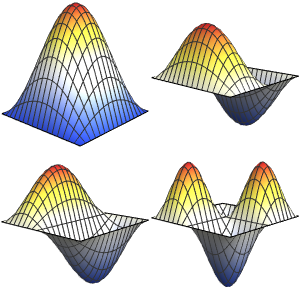
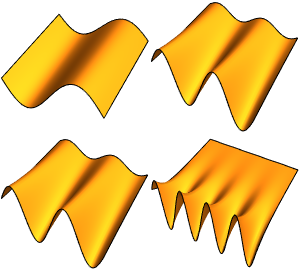
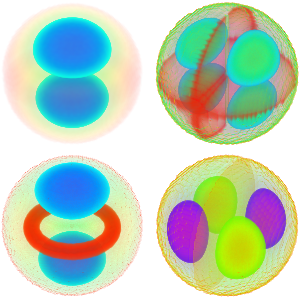
A Laplacian's Eigenvalues & Eigenfunctions
Find the four smallest eigenvalues and eigenfunctions of a Laplacian operator, i.e. solutions to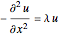 
, over a 1D region.
Specify a Laplacian.
In[1]:=
\[ScriptCapitalL] = -Laplacian[u[x], {x}];Numerically find the four smallest eigenvalues and eigenfunctions.
In[2]:=
NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4]Out[2]=
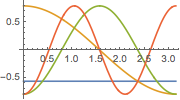
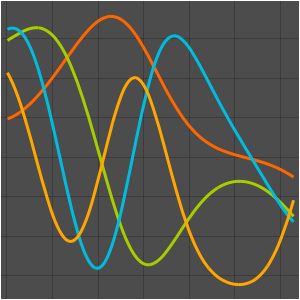
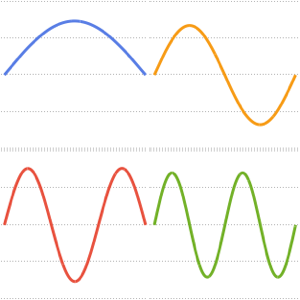
Visualize the eigenfunctions.
In[3]:=
NDEigensystem[\[ScriptCapitalL], u[x], {x, 0, \[Pi]}, 4];
Plot[Evaluate[%[[2]]], {x, 0, \[Pi]}]Out[3]=
