Wolfram Language™

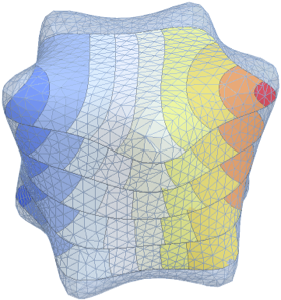
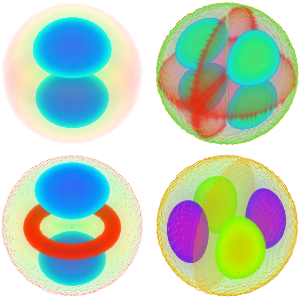
Investige una ecuación de Laplace en un toro

Encuentre los cinco valores propios y funciones propias de una ecuación de Laplace en un toro cuadrado con una condición de Dirichlet.

Especifique las condiciones de límite periódicas en un cuadrado de longitud 1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Especifique un valor en el origen. Por las condiciones periódicas, este debe ser el valor en las otras tres aristas del cuadrado.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Calcule los valores propios y funciones propias.

In[3]:=

{vals, funs} = NDEigensystem[ Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Inspecciones los valores propios.

In[4]:=

vals

Out[4]=

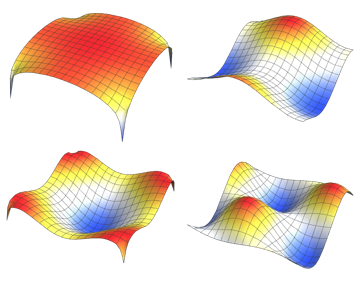
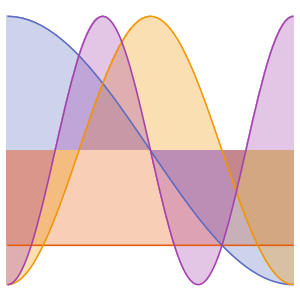
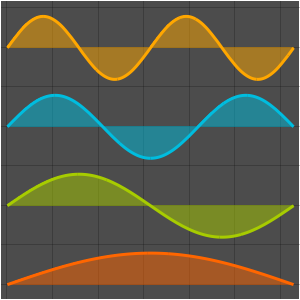
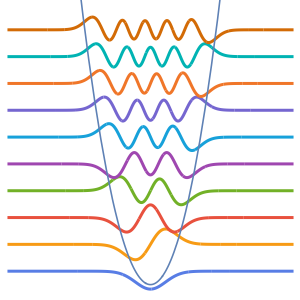
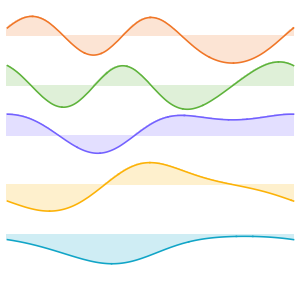
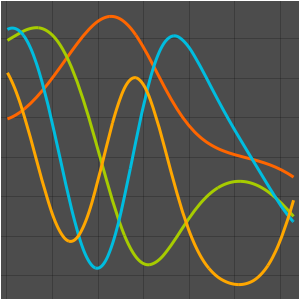
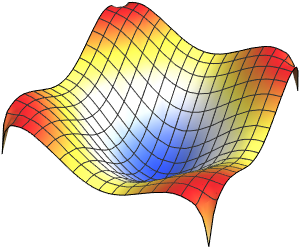
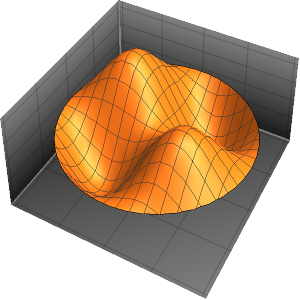
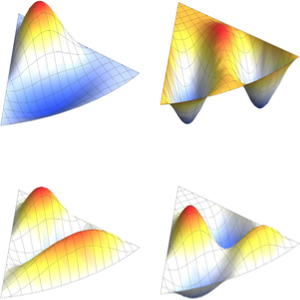
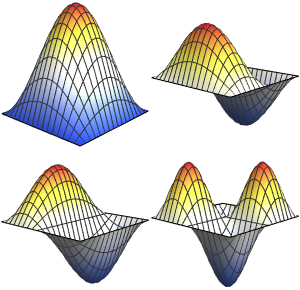
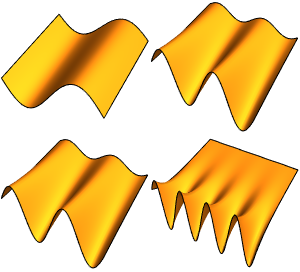
Visualice las funciones propias.

In[5]:=

ImageCollage[ Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ funs, Background -> Transparent]

Out[5]=