Analice un operador de Sturm–Liouville con potencial asimétrico

Encuentre los cinco valores propios y funciones propias periódicos más pequeños de un operador de Sturm–Liouville.

Especifique un operador de Sturm–Liouville.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

Especifique una condición de límite periódica.

In[2]:=

\[ScriptCapitalB] = u[0] == u[2 \[Pi]];

Encuentre los cinco valores propios y funciones propias más pequeños.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

Inspeccione los valores propios.

In[4]:=

vals

Out[4]=

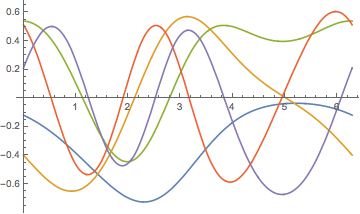
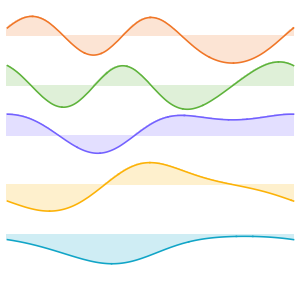
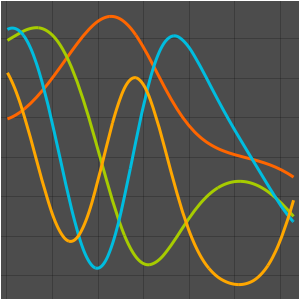
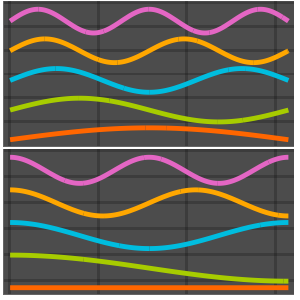
Visualice las funciones propias.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=