Encuentre los valores propios de Aharonov–Bohm
El efecto de Aharonov–Bohm es un fenómeno mecánico cuántico donde una partícula cargada detecta un potencial de calibre electromagnético, a pesar de que el campo magnético dentro de la región donde la partícula se mueve es cero. En este ejemplo, se considera la ecuación de Schrödinger para un campo magnético fijo concentrado en una línea perpendicular al dominio de la partícula.
Especifique la región como un sector en el plano 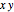 centrado cerca del eje
centrado cerca del eje 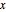 .
.
In[1]:=
\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];Especifique el operador de Aharonov–Bohm. El campo magnético está restringido al eje 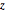 .
.
In[2]:=
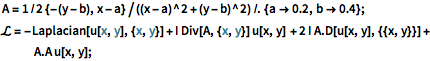
A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2,
b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] +
I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] +
A.A u[x, y];Especifique las condiciones de límite en el límite completo.
In[3]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];Calcule seis valores propios y funciones propias del operador.
In[4]:=
{vals, funs} =
NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y], {x, y} \[Element] \[CapitalOmega], 6]; Inspeccione los valores propios.
In[5]:=
valsOut[5]=
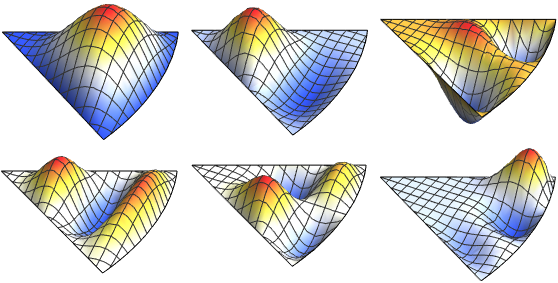
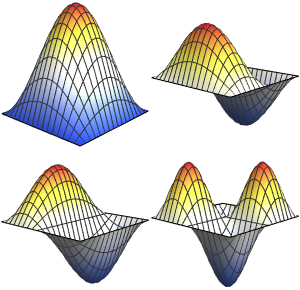
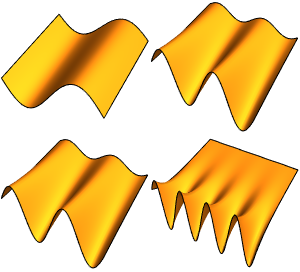
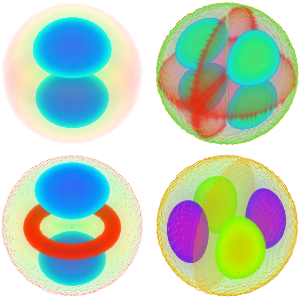
Visualice la parte real de las funciones propias.
muestre la entrada completa de Wolfram Language
Out[6]=