Wolfram Language™

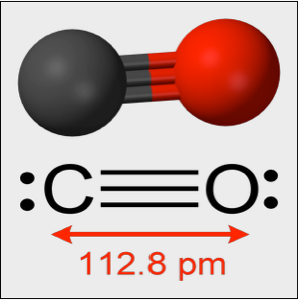
Modele oscilaciones pequeñas en una molécula de CO

Experimentalmente, una molécula de CO oscila alrededor de su longitud de equilibrio con un constante efectiva de elasticidad de . Las oscilaciones están gobernadas por una ecuación de oscilador armónica cuántica. En el siguiente ejemplo, es la masa reducida de la molécula, es la frecuencia natural, 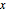el desplazamiento de la posición de equilibrio, y 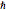es la constante reducida de Planck.

In[1]:=

qho = -(\[HBar]^2/(2 m)) Laplacian[u[x], {x}] + (m \[Omega]^2)/ 2 x^2 u[x];

Calcule los primeros cuatro valores propios y funciones propias normalizadas.

In[2]:=

sol = DEigensystem[qho, u[x], {x, -\[Infinity], \[Infinity]}, 4, Assumptions -> \[HBar] > 0 && m > 0 && \[Omega] > 0, Method -> "Normalize"]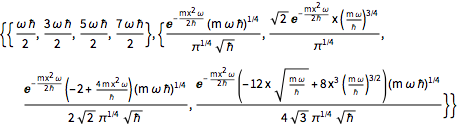

Out[2]=

Suponiendo que la partícula está en una superposición igual de los cuatro estados, la función de onda tendrá la forma .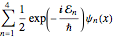

In[3]:=

\[Psi][x_, t_] = Total[MapThread[1/2 Exp[I E t #1/\[HBar]] #2 &, sol]]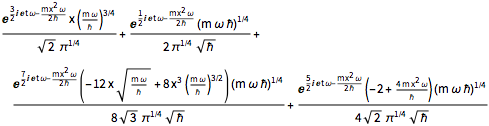

Out[3]=

Calcule los tres parámetros 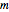, 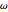y 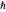usando como unidades base, unidades de masa atómica, femtosegundos y picómetros, mientras los valores resultantes estarán más cerca a la unidad de orden.

In[4]:=

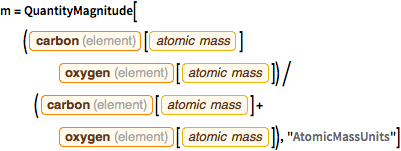
m = QuantityMagnitude[( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] Entity["Element", "Oxygen"][EntityProperty["Element", "AtomicMass"]])/( Entity["Element", "Carbon"][ EntityProperty["Element", "AtomicMass"]] + Entity["Element", "Oxygen"][ EntityProperty["Element", "AtomicMass"]]), "AtomicMassUnits"]

Out[4]=

In[5]:=

\[Omega] = Sqrt[QuantityMagnitude[Quantity[1.86, "Kilonewtons"/"Meters"], "AtomicMassUnit"/"Femtoseconds"^2]/m]

Out[5]=

In[6]:=

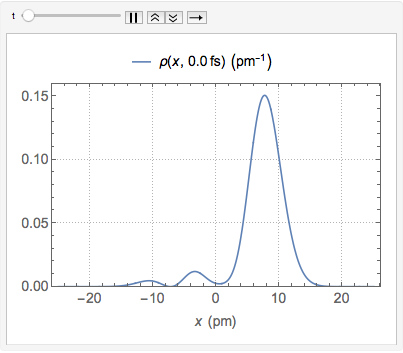
\[HBar] = QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], "AtomicMassUnit"*"Picometers"^2/"Femtoseconds"]

Out[6]=

La función de densidad de probabilidad del desplazamiento es dada por .

In[7]:=

\[Rho][x_, t_] = FullSimplify[ComplexExpand[Conjugate[\[Psi][x, t]] \[Psi][x, t]]]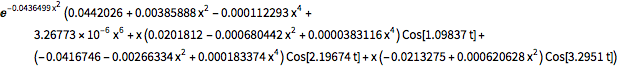

Out[7]=

Como una distribución de probabilidad, la integral de sobre los reales es 1 para todo .

In[8]:=

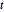Chop[Integrate[\[Rho][x, t], {x, -\[Infinity], \[Infinity]}]]

Out[8]=

Visualice la densidad de probabilidad en el tiempo.

In[9]:=

Animate[Plot[\[Rho][x, t], {x, -25, 25}, PlotRange -> {0, .16}, PlotTheme -> "Detailed", FrameLabel -> {Row[{x, RawBoxes@RowBox[{"(", "\"pm\"", ")"}]}, " "], None}, LabelStyle -> Larger, PlotLegends -> Placed[{Row[{HoldForm[\[Rho]][x, Quantity[NumberForm[t, {2, 1}], "Femtoseconds"]], RawBoxes@RowBox[{"(", SuperscriptBox["\"pm\"", -1], ")"}]}, " "]}, Above]], {t, 0., 5.7, ImageSize -> Small}, AnimationRate -> 1, SaveDefinitions -> True, Alignment -> Center]

Reproducir

Detener