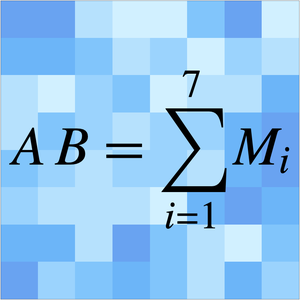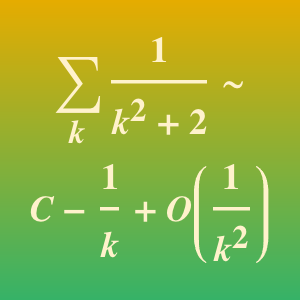計算の複雑性を求める
アルゴリズムのランタイムを語るとき，厳密なランタイム関数にAsymptoticEqual (big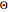 
)である最も簡単な関数を与えるのが通例である．この等価性を記述する別の方法として，それぞれの関数がもう一方の関数よりAsymptoticLessEqual (big 
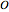)かつAsymptoticGreaterEqual (big 
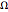)であるというものがある．この概念は，部分行列の掛け算について最初に発見されたアルゴリズムであるシュトラッセン（Strassen）のアルゴリズムに示されている．
このアルゴリズムは4つのステップからなる．その4つとは，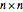
行列のそれぞれを4個の部分行列に分割し，8個の部分行列から14の線形結合を形成し，このうちの7個のペアを乗算し，7個の結果を合計するというものである．したがって，乗算を行う時間 
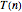は行列を分割する一定時間 
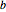，2番目と4番目のステップで線形結合を形成する時間
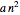，3番目のステップの時間
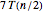である．
再帰関係を解く．
結果は複雑であるが，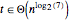
である．
同様に 
，
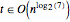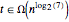である．
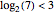なので，アルゴリズムは次数3以下である．
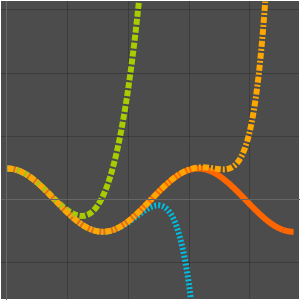
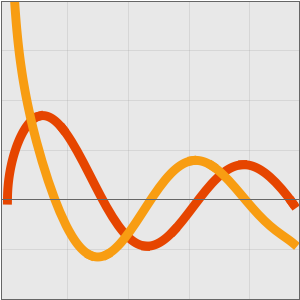
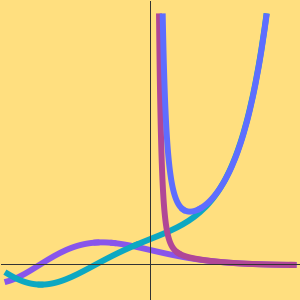
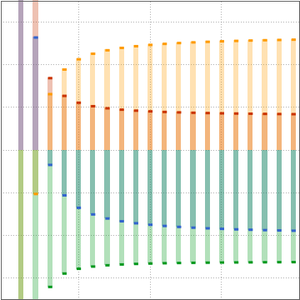
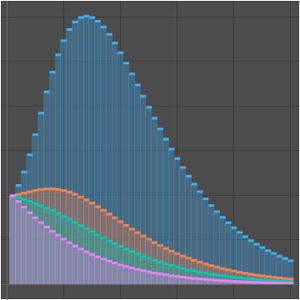
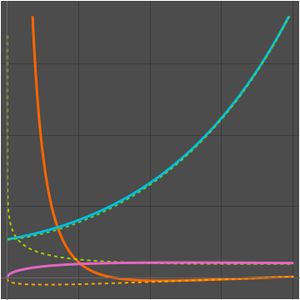
単純な三次アルゴリズムとシュトラッセンのアルゴリズムの成長率を比較する．
