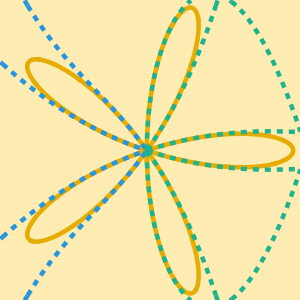
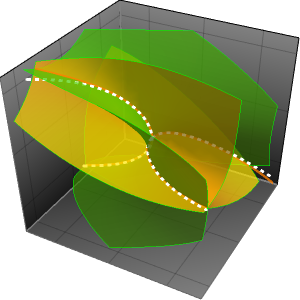
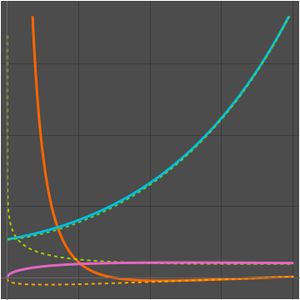
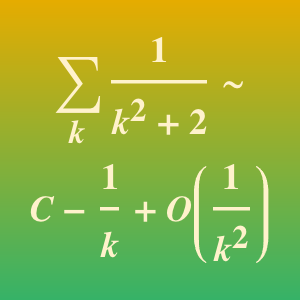漸近関係を使ってアルゴリズムを比較する
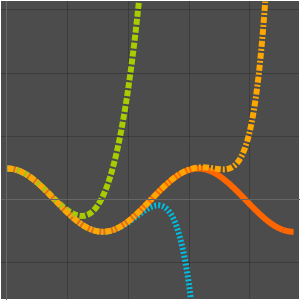
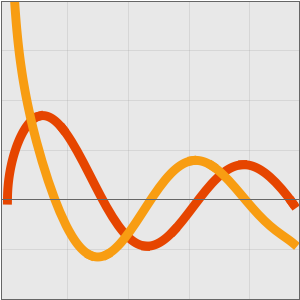
アルゴリズムは,計算的複雑性では,大規模な入力(通常無限大と考えられる)に対する挙動によって分類される.2つのアルゴリズムは、一方のランタイムがAsymptoticLessEqual (big  ),AsymptoticLess (little
),AsymptoticLess (little 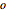 ),AsymptoticGreaterEqual (big
),AsymptoticGreaterEqual (big 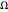 ),AsymptoticGreater (little
),AsymptoticGreater (little 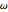 )のどれであるかによって比較される.
)のどれであるかによって比較される.
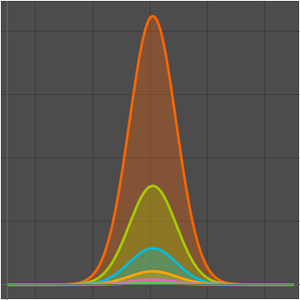
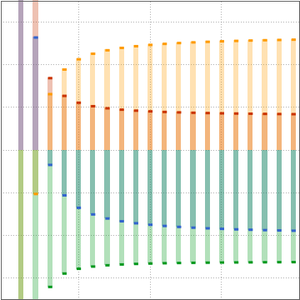
巡回セールスマン問題(TSP)は, 個の都市を繋いだ最短距離を求めることである.単純なアルゴリズムは
個の都市を繋いだ最短距離を求めることである.単純なアルゴリズムは  種類の経路をすべて試してみることである.Held–Karpアルゴリズムは,それを向上させておよそ
種類の経路をすべて試してみることである.Held–Karpアルゴリズムは,それを向上させておよそ 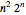 ステップにしたものである.
ステップにしたものである.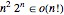 を示すとHeld–Karpアルゴリズムの方が速いことがわかる.
を示すとHeld–Karpアルゴリズムの方が速いことがわかる.
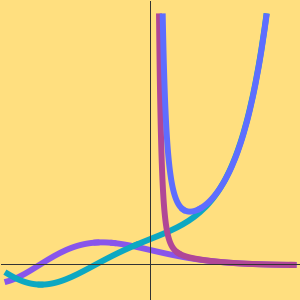
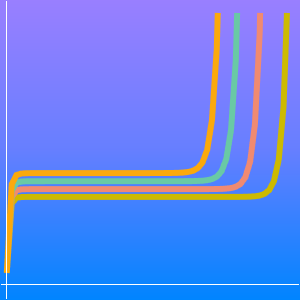
どちらのアルゴリズムも,巡回セールスマン問題の複雑性のクラスが,時間 で解ける問題のEXPTIMEほど悪くないことを示している.例えば任意の
で解ける問題のEXPTIMEほど悪くないことを示している.例えば任意の  では
では 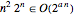 なので,Held–Karpアルゴリズムは指数的ランタイムを持つ.
なので,Held–Karpアルゴリズムは指数的ランタイムを持つ.
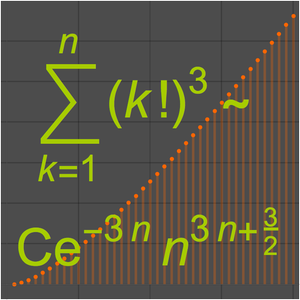
階乗関数の場合,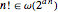 なので線形指数では不十分である.
なので線形指数では不十分である.
しかし, なので階乗関数はまだ指数的ランタイムを持つ.
なので階乗関数はまだ指数的ランタイムを持つ.
近似解は 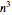 の時間で見付けられるため,近似の巡回セールスマン問題は多項式時間で解ける問題である複雑性クラスPである.どの多項式アルゴリズムも指数アルゴリズムより速い.つまり
の時間で見付けられるため,近似の巡回セールスマン問題は多項式時間で解ける問題である複雑性クラスPである.どの多項式アルゴリズムも指数アルゴリズムより速い.つまり .
.