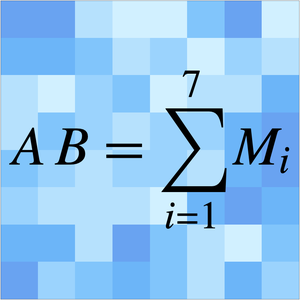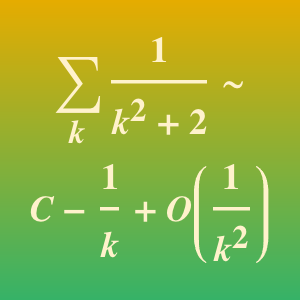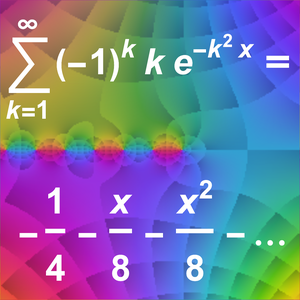発散する漸近展開を調べる(AsymptoticIntegrate)
漸近展開は発散級数で与えられることが多い．通常発散級数の最初の数項は問題に対するよい近似を提供するが，級数の項数が増えるにつれて近似の質は低下する．パラメータに依存する定積分の例で，この現象を説明する．
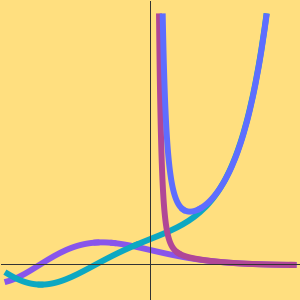
次の定積分の級数展開を考える．
この級数は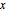 
の非零の値すべてについて発散する．
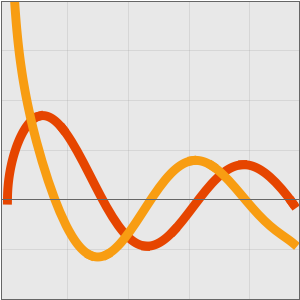
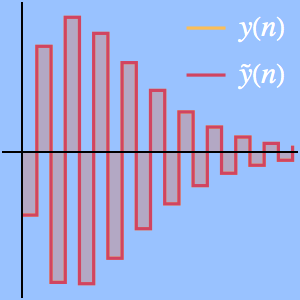
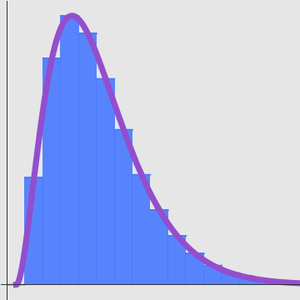
この級数は発散するが，積分に対するすばらしい漸近近似を提供する．たとえば，次の数値比較によると，この近似はかなり正確である．
項の数が多くなると，近似は正確ではなくなる．これは漸近級数ではよくある挙動である．
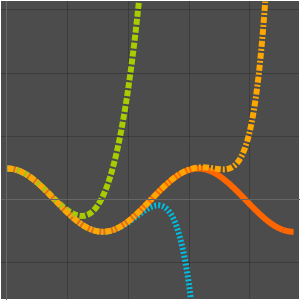
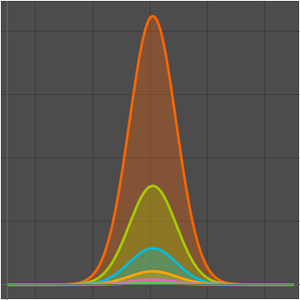
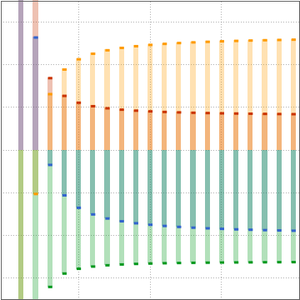
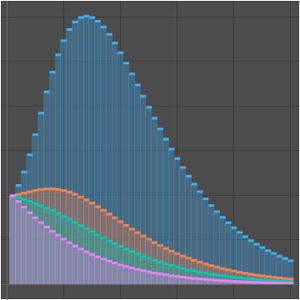
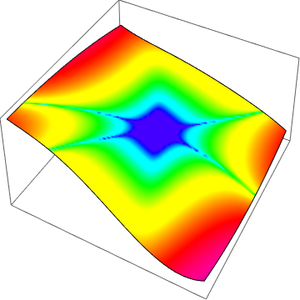
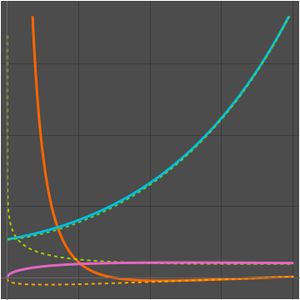
次のプロットは，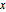
の固定された値について，項の数が一定範囲（
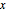に依存）内にある場合，漸近級数はよい近似を与えるということを示している．項の数がこの範囲を超えて増加すると，近似は発散し始める．
完全なWolfram言語入力を表示する
IntegrateあるいはRegularizationを使って，厳密な結果を得る．
