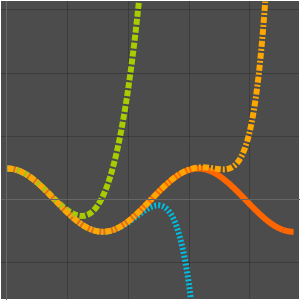
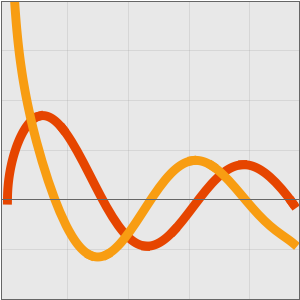
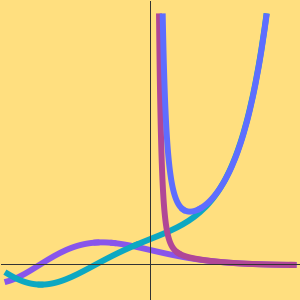
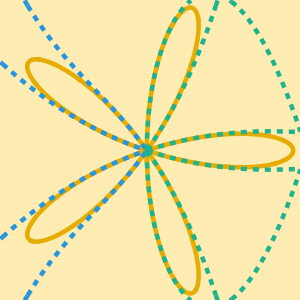
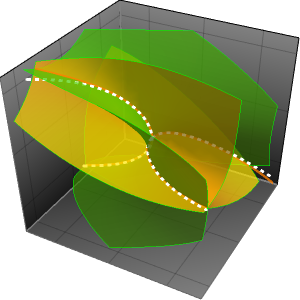
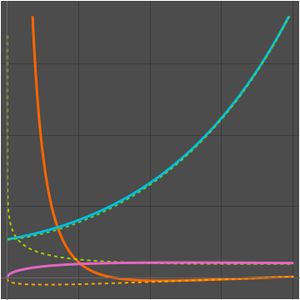
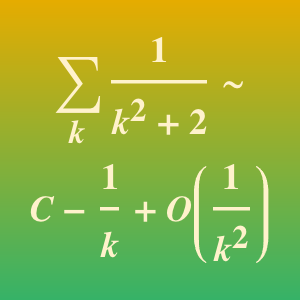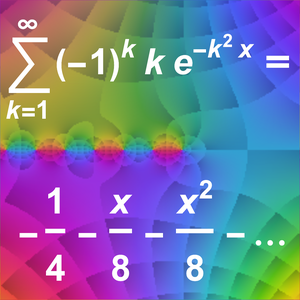漸近近似を検証する
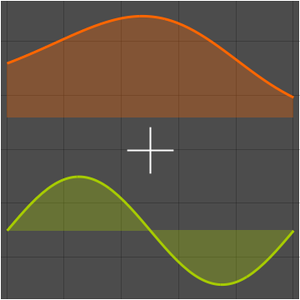
関数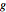 
が，基点に近付くにつれて消失する相対誤差を持つ関数 
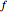を近似するならば，
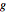は 
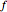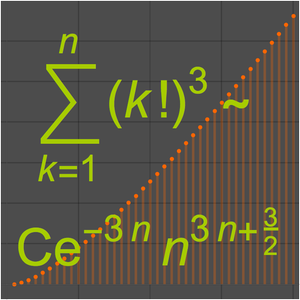
と漸近的に等価（AsymptoticEquivalent）である（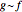
と書かれることがある）と言われる．よくある例として，階乗関数のスターリング(Stirling)の近似がある．
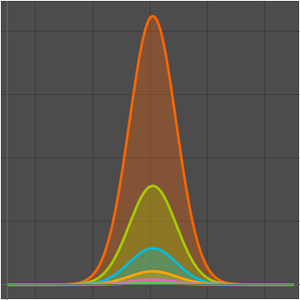
相対誤差がゼロに近付くので，関数の割合は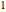
に近付く．
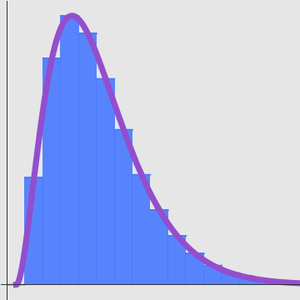
スターリングの近似では，相対誤差が0に近付くと，絶対誤差が無限大に近付く．
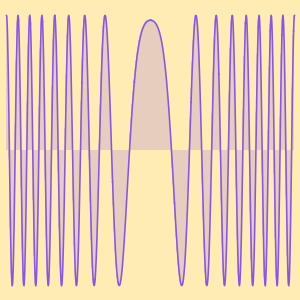
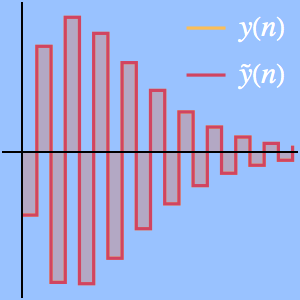
テイラー(Taylor)級数は漸近近似を与える．
ローラン(Laurent)級数も漸近近似を与える．
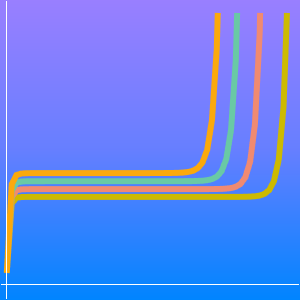
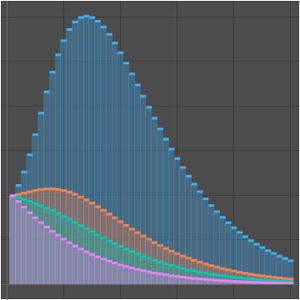
素数定理によると，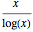
は素数計数関数 
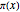の漸近近似である．
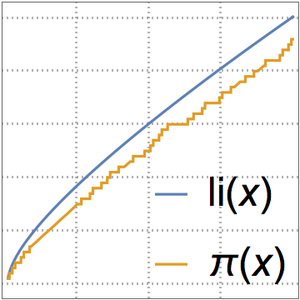
対数積分関数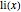
でよりよい近似が与えられる．
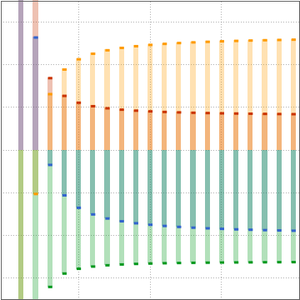
素数計数関数と2つの近似を比較する．
