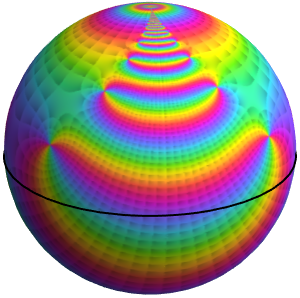
La sphère de Riemann
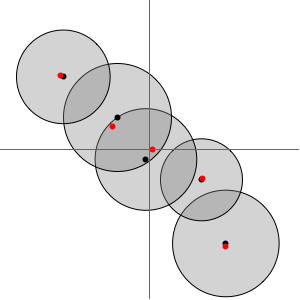
Projetez le plan complexe prolongé (http://mathworld.wolfram.com/ExtendedComplexPlane.html) sur une sphère, de sorte que le plan au complet soit visible, y compris le point à l'infini.
Un point  dans le plan complexe est représenté sur la sphère de Riemann en projetant
dans le plan complexe est représenté sur la sphère de Riemann en projetant 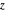 jusqu'au point d'intersection de la sphère et de la ligne allant de
jusqu'au point d'intersection de la sphère et de la ligne allant de 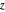 jusqu'au pôle nord de la sphère.
jusqu'au pôle nord de la sphère.
Si la sphère est décrite de façon paramétrique comme suit : 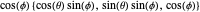 ,
, 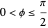 ,
, 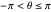 , alors un point sur la sphère correspond au point
, alors un point sur la sphère correspond au point 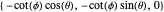 dans le plan.
dans le plan.
Définissez une fonction 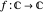 à projeter sur la sphère.
à projeter sur la sphère.
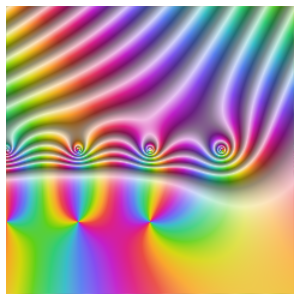
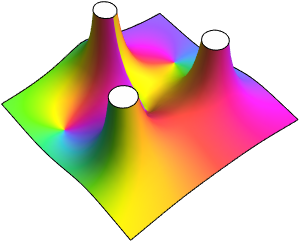
Utilisez ComplexPlot afin de créer une texture pour la sphère de Riemann, en utilisant 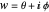 .
.
Représentez graphiquement la sphère de Riemann texturée et son équateur correspondant à la projection du cercle unitaire dans le plan complexe.
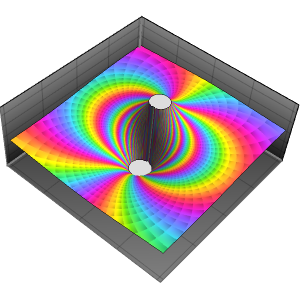
Utilisez ComplexPlot afin de créer une texture pour le plan complexe intégré dans un espace tridimensionnel.
Appliquez la texture plane complexe au plan 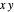 .
.
Affichez le plan et la sphère ensemble. Le cercle unitaire dans le plan correspond à l'équateur sur la sphère.