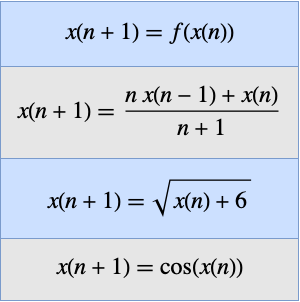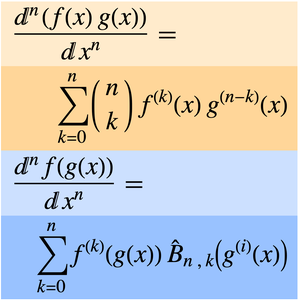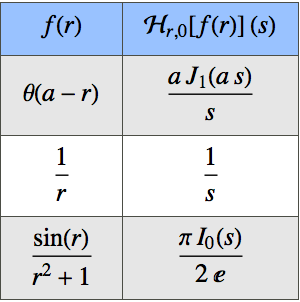Die Schwingungen von n-ten Ableitungen untersuchen
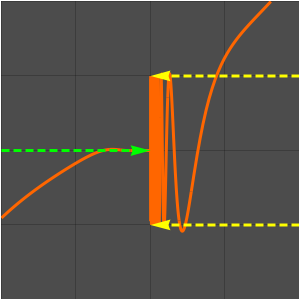
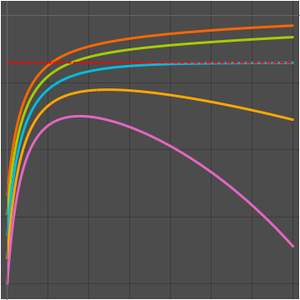
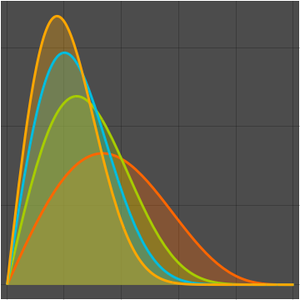
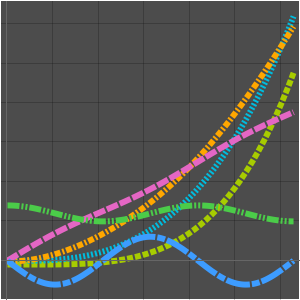
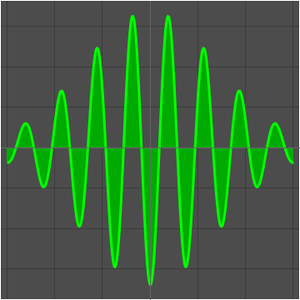
Dieses Beispiel zeigt, wie die höheren Ableitungen einer Funktion Schwingungen erzeugen. Mit zunehmender Ordung der Ableitungen belegen die Schwingungen immer größere Intervalle auf der reellen Zahlengerade.
Ermitteln Sie die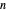 
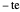Ableitung einer Gaußschen Exponentialfunktion.
Die geschlossene Form der Ableitung kann auch in ein Hermitesches Polynom umgewandelt werden.
Die Ableitungen höherer Ordnung der Gauß-Funktion erzeugen Schwingungen, wie im Folgenden gezeigt wird:
Mit diesen Ableitungen werden in der Bildverarbeitung Gauß-Filter erzeugt.
