核心算法
群论算法
Mathematica 8 新增了应用于置换和置换群的函数及算法。这是在 Mathematica 中首次提供对大量群的系统访问,这些群可通过置换集合相乘来构造。
- 支持由不相交轮换表示的置换。
- 支持由置换集合产生的群。具有群的无限族和散在群的预存生成元。
- 以乘法表或凯莱图可视化群。
- 计算轨道、稳定子、中心化子、陪集表示等。
 |  |  |
| 计算群的乘法表 » | 群的凯莱图表示 » | 被群中递增置换所移动的点 » |
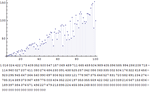 | 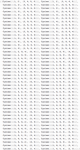 | 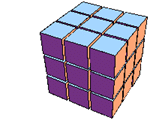 |
| 具有随机生成元的群的阶数 » | 计算一个置换群某元素的共轭类 » | 3x3x3 Rubik 魔方群的稳定子群链 » |
相关函数Cycles  PermutationCycles
PermutationCycles  PermutationCyclesQ
PermutationCyclesQ  PermutationList
PermutationList  PermutationListQ
PermutationListQ  RandomPermutation
RandomPermutation  Permute
Permute  FindPermutation
FindPermutation  PermutationReplace
PermutationReplace  PermutationSupport
PermutationSupport  PermutationMax
PermutationMax  PermutationMin
PermutationMin  PermutationLength
PermutationLength  PermutationProduct
PermutationProduct  InversePermutation
InversePermutation  PermutationPower
PermutationPower  PermutationOrder
PermutationOrder  PermutationGroup
PermutationGroup  GroupGenerators
GroupGenerators  GroupOrder
GroupOrder  GroupElements
GroupElements  GroupElementQ
GroupElementQ  GroupElementPosition
GroupElementPosition  GroupMultiplicationTable
GroupMultiplicationTable  CayleyGraph
CayleyGraph  GroupOrbits
GroupOrbits  GroupStabilizer
GroupStabilizer  GroupSetwiseStabilizer
GroupSetwiseStabilizer  GroupActionBase
GroupActionBase  GroupStabilizerChain
GroupStabilizerChain  GroupCentralizer
GroupCentralizer  RightCosetRepresentative
RightCosetRepresentative  SymmetricGroup
SymmetricGroup  AlternatingGroup
AlternatingGroup  DihedralGroup
DihedralGroup  CyclicGroup
CyclicGroup  AbelianGroup
AbelianGroup  MathieuGroupM11
MathieuGroupM11  MathieuGroupM12
MathieuGroupM12  MathieuGroupM22
MathieuGroupM22  MathieuGroupM23
MathieuGroupM23  MathieuGroupM24
MathieuGroupM24  JankoGroupJ1
JankoGroupJ1  JankoGroupJ2
JankoGroupJ2  JankoGroupJ3
JankoGroupJ3  JankoGroupJ4
JankoGroupJ4  ConwayGroupCo1
ConwayGroupCo1  ConwayGroupCo2
ConwayGroupCo2  ConwayGroupCo3
ConwayGroupCo3  FischerGroupFi22
FischerGroupFi22  FischerGroupFi23
FischerGroupFi23  FischerGroupFi24Prime
FischerGroupFi24Prime  HigmanSimsGroupHS
HigmanSimsGroupHS  McLaughlinGroupMcL
McLaughlinGroupMcL  SuzukiGroupSuz
SuzukiGroupSuz  HeldGroupHe
HeldGroupHe  HaradaNortonGroupHN
HaradaNortonGroupHN  ThompsonGroupTh
ThompsonGroupTh  BabyMonsterGroupB
BabyMonsterGroupB  MonsterGroupM
MonsterGroupM  ONanGroupON
ONanGroupON  RudvalisGroupRu
RudvalisGroupRu  LyonsGroupLy
LyonsGroupLy  TitsGroupT
TitsGroupT
 PermutationCycles
PermutationCycles  PermutationCyclesQ
PermutationCyclesQ  PermutationList
PermutationList  PermutationListQ
PermutationListQ  RandomPermutation
RandomPermutation  Permute
Permute  FindPermutation
FindPermutation  PermutationReplace
PermutationReplace  PermutationSupport
PermutationSupport  PermutationMax
PermutationMax  PermutationMin
PermutationMin  PermutationLength
PermutationLength  PermutationProduct
PermutationProduct  InversePermutation
InversePermutation  PermutationPower
PermutationPower  PermutationOrder
PermutationOrder  PermutationGroup
PermutationGroup  GroupGenerators
GroupGenerators  GroupOrder
GroupOrder  GroupElements
GroupElements  GroupElementQ
GroupElementQ  GroupElementPosition
GroupElementPosition  GroupMultiplicationTable
GroupMultiplicationTable  CayleyGraph
CayleyGraph  GroupOrbits
GroupOrbits  GroupStabilizer
GroupStabilizer  GroupSetwiseStabilizer
GroupSetwiseStabilizer  GroupActionBase
GroupActionBase  GroupStabilizerChain
GroupStabilizerChain  GroupCentralizer
GroupCentralizer  RightCosetRepresentative
RightCosetRepresentative  SymmetricGroup
SymmetricGroup  AlternatingGroup
AlternatingGroup  DihedralGroup
DihedralGroup  CyclicGroup
CyclicGroup  AbelianGroup
AbelianGroup  MathieuGroupM11
MathieuGroupM11  MathieuGroupM12
MathieuGroupM12  MathieuGroupM22
MathieuGroupM22  MathieuGroupM23
MathieuGroupM23  MathieuGroupM24
MathieuGroupM24  JankoGroupJ1
JankoGroupJ1  JankoGroupJ2
JankoGroupJ2  JankoGroupJ3
JankoGroupJ3  JankoGroupJ4
JankoGroupJ4  ConwayGroupCo1
ConwayGroupCo1  ConwayGroupCo2
ConwayGroupCo2  ConwayGroupCo3
ConwayGroupCo3  FischerGroupFi22
FischerGroupFi22  FischerGroupFi23
FischerGroupFi23  FischerGroupFi24Prime
FischerGroupFi24Prime  HigmanSimsGroupHS
HigmanSimsGroupHS  McLaughlinGroupMcL
McLaughlinGroupMcL  SuzukiGroupSuz
SuzukiGroupSuz  HeldGroupHe
HeldGroupHe  HaradaNortonGroupHN
HaradaNortonGroupHN  ThompsonGroupTh
ThompsonGroupTh  BabyMonsterGroupB
BabyMonsterGroupB  MonsterGroupM
MonsterGroupM  ONanGroupON
ONanGroupON  RudvalisGroupRu
RudvalisGroupRu  LyonsGroupLy
LyonsGroupLy  TitsGroupT
TitsGroupT参见8 的新功能
有问题?获取个人回复。
|





