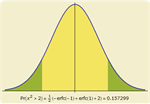
基于20多年精心开发的符号和数值算法，Mathematica 8 提供一整套高级的概率和统计函数。新的功能包括计算任何事件的概率或任何表达式的期望，模拟任何分布以及自动估计参数或测试分布的拟合优度。 为了更好地支持分布模型，并对其进行分析，Mathematica 8 提供大量概率分布函数，以及对数十个属性的完全支持，包括分布函数、矩、分位数和母函数。

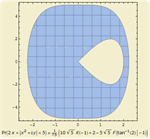
• 以方程组和不等式的逻辑组合形式，对概率和条件概率进行符号和数值计算。 »
• 表达式的期望和条件期望的符号和数值计算。 »
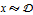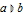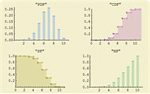
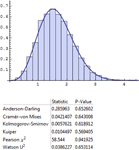
• 用于分布 () 和条件 () 的排版字符。 »
• 自动支持模拟分布、估计分布中的参数以及测试分布的拟合优度。 »
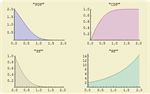
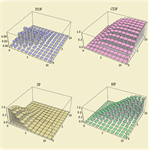
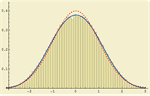
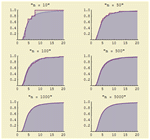
• 直接支持多个不同分布函数，包括概率密度函数、累积分布函数、生存、风险、逆累积分布和逆生存函数。 »
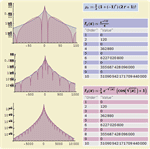
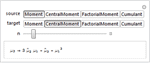
• 直接支持多个不同类型的矩，包括原矩、中心矩、累积量和阶乘矩。 »
• 直接支持所有与矩相关的母函数，包括矩母函数和累积量母函数。 »
• 在不同类型的矩间自动转换。 »
• 自动计算标准和无偏矩估计量。 »

计算事件的概率 »	计算表达式的期望 »	计算条件概率和期望 »
计算双尾概率 »	元件的使用寿命 »	求人类染色体的期望长度 »
求相遇的概率 »	单变量连续分布函数 »	单变量离散分布函数 »
双变量连续分布函数 »	双变量离散分布函数 »	采用 Edgeworth 展开逼近分布 »
演示 Glivenko-Cantelli 定理 »	计算复概率 »	研究离差和位置度量 »
使用同样的矩序列比较两个分布 »	求特征函数的解析解 »	从矩中求多变量累积量 »
构建无偏估计量 »	在正式矩间转换 »	求样本估计量多项式的期望 »
参数估计和拟合优度检验 »

相关函数

Probability  NProbability  Expectation  NExpectation  EstimatedDistribution  FindDistributionParameters  RandomVariate  DistributionFitTest  PDF  CDF  SurvivalFunction  HazardFunction  InverseCDF  InverseSurvivalFunction  Quantile  Moment  CentralMoment  FactorialMoment  Cumulant  MomentGeneratingFunction  CentralMomentGeneratingFunction  FactorialMomentGeneratingFunction  CumulantGeneratingFunction  MomentConvert  MomentEvaluate  Mean  Variance  StandardDeviation  Skewness  Kurtosis  Covariance  Correlation  Median