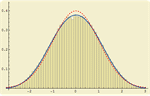
Construído ao longo de duas décadas e com algoritmos numéricos e simbólicos desenvolvidos, o Mathematica 8 oferece um conjunto de funções de alto nível para probabilidade e estatística. Novos recursos, incluindo a habilidade de computar a probabilidade de qualquer evento ou a expectativa de qualquer expressão, simular qualquer distribuição, e estimar parâmetros automaticamente ou testar a compatibilidade de certo ajuste com distribuições. Para suportar a modelagem e análise, o Mathematica 8 oferece a maior coleção de distribuições probabilísticas, assim como suporte completo a diversas propriedades, incluindo distribuição de funções, momentos, cuantis e geração de funções.

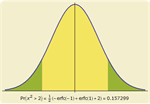
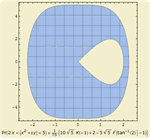
• Computação simbólica e numérica de probabilidades e condições probabilísticas de eventos como combinações lógicas e inequações. »
• Computação simbólica e numérica de expectativas e expectativas condicionais de expressões. »
• Formatação de caracteres para distribuições (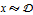) e condições (). »
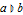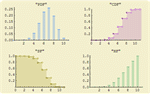
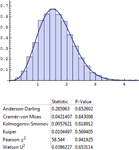
• Suporte automático para simulação de distribuições, estimação de parâmetros em distribuições, e teste da compatibilidade de ajustes para distribuições. »
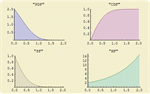
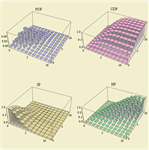
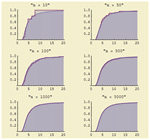
• Suporte direto a diversas funções de distribuição diferentes incluindo distribuição de probabilidade, CDF, sobrevivência, risco CDF inverso, e funções de sobrevivência inversas. »
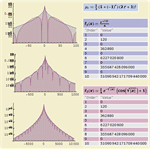
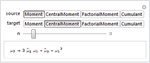
• Suporte direto a diferentes tipos de momentos incluindo "raw moments", momentos centrais, cumulantes e momentos fatoriais. »
• Suporte direto a todas as funções generativas associadas com momentos, incluindo funções geradoras de momentos e funções geradoras de cumulantes. »
• Conversão automática entre diferentes tipos de momentos. »
• Computação automática de estimadores de momentos padrão e imparcial. »

Compute a probabilidade de um evento »	Compute a Expectativa de uma Função »	Compute Probabilidades Condicionais e Expectativas »
Compute a Probabilidade de Duas Caudas »	Vida de um Componente »	Encontre o Comprimento Esperado de um Cromossomo Humano »
Encontre a Probabilidade de um Encontro »	Funções de Distribuição Contínua Univariada »	Funções de Distribuição Discreta Univariada »
Funções de Distribuição Contínua Bivariadas »	Funções de Distribuição Discreta Bivariada »	Execute Expansões de Edgeworth para Aproximar Distribuições »
Demonstre o Teorema de Glivenko-Cantelli »	Compute Probabilidades Complexas »	Estude Dispersão e Medidas Locais »
Compare Duas Distribuições com a Mesma Sequência de Momento »	Encontre uma Função Fechada para a Função Característica »	Encontre Cumulantes Multivariados a partir de Momentos »
Construa Estimadores Imparciais »	Faça a Conversão entre Momentos Formais »	Encontre as Expectativas de Estimadores Padrão de Polinômios »
Estime Parâmetros e Teste a Compatibilidade de um Ajuste »

FUNÇÕES RELACIONADAS

Probability  NProbability  Expectation  NExpectation  EstimatedDistribution  FindDistributionParameters  RandomVariate  DistributionFitTest  PDF  CDF  SurvivalFunction  HazardFunction  InverseCDF  InverseSurvivalFunction  Quantile  Moment  CentralMoment  FactorialMoment  Cumulant  MomentGeneratingFunction  CentralMomentGeneratingFunction  FactorialMomentGeneratingFunction  CumulantGeneratingFunction  MomentConvert  MomentEvaluate  Mean  Variance  StandardDeviation  Skewness  Kurtosis  Covariance  Correlation  Median