라플라스 방정식의 디리클레 문제 해결

이차원의 라플라스 방정식을 지정합니다.

In[1]:=

leqn = Laplacian[u[x, y], {x, y}] == 0;

직사각형의 방정식에 대한 디리클레 조건을 규정합니다.

In[2]:=

\[CapitalOmega] = Rectangle[{0, 0}, {1, 2}];

In[3]:=

dcond = DirichletCondition[ u[x, y] == Piecewise[{{UnitTriangle[2 x - 1], y == 0 || y == 2}}, 0], True];

디리클레 문제를 해결합니다.

In[4]:=

sol = DSolveValue[{leqn, dcond}, u[x, y], {x, y} \[Element] \[CapitalOmega]] // FullSimplify

Out[4]=

Inactive의 합에서 처음 300항을 추출합니다.

In[5]:=

asol = sol /. {\[Infinity] -> 300} // Activate;

직사각형의 솔루션을 시각화합니다.

In[6]:=

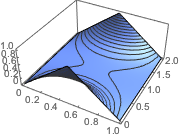
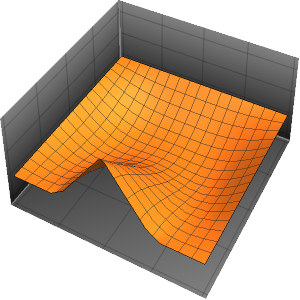
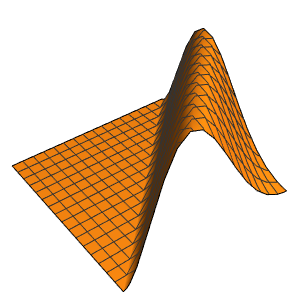
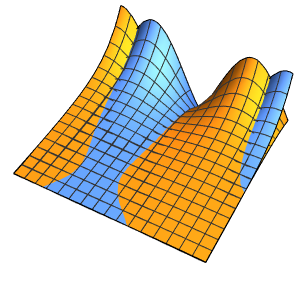
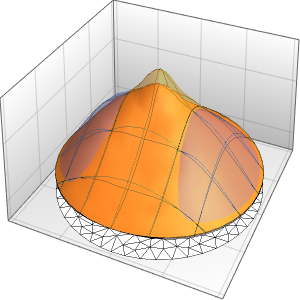
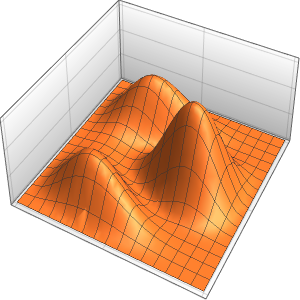
Plot3D[asol // Evaluate, {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotTheme -> "Business"]

Out[6]=