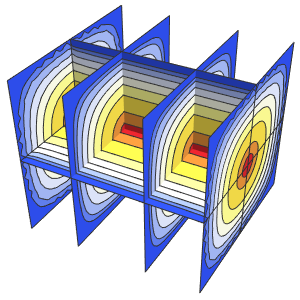
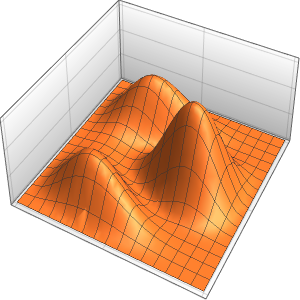
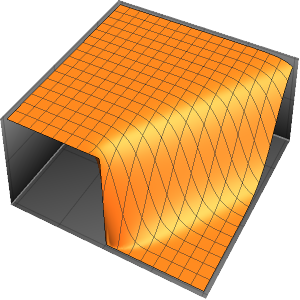
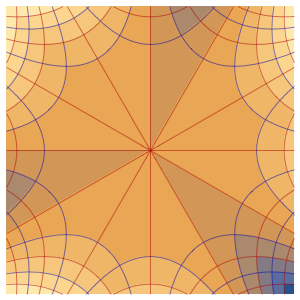
이벤트가있는 편미분 방정식을 영역에서 해결: Wolfram Language 11의 신기능

이벤트가있는 편미분 방정식을 영역에서 해결

삼중 단열 벽과 외부 온도의 영향을 받는 유리 정면 현관을 가진 방에서 온도 제어된 발열을 모델링합니다.

In[1]:=

\[CapitalOmega] = Rectangle[{0, 0}, {3/2, 1}];
outsideTemp[t_] := 15 + 10*Sin[2 \[Pi] t/24];
kd = 0.78; Ld = 0.05;
\[CapitalGamma] = 
  NeumannValue[Ld/kd*(outsideTemp[t] - u[t, x, y]), {x == 0}];

난방기의 부하는 사건에 의해 증가하거나 감소합니다.

In[2]:=

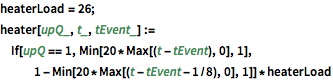
heaterLoad = 26;
heater[upQ_, t_, tEvent_] := 
 If[upQ == 1, Min[20*Max[(t - tEvent), 0], 1], 
   1 - Min[20*Max[(t - tEvent - 1/8), 0], 1]]*heaterLoad

편미분 방정식은 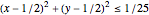사이클에서 열을 생성하고 유리 창문을 통해 열을 잃는 동안 공기를 통한 열 확산을 모델링합니다.

In[3]:=

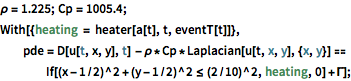
\[Rho] = 1.225; Cp = 1005.4;
With[{heating = heater[a[t], t, eventT[t]]},
  pde = D[u[t, x, y], t] - \[Rho]*Cp*Laplacian[u[t, x, y], {x, y}] == 
    If[(x - 1/2)^2 + (y - 1/2)^2 <= (2/10)^2, heating, 
      0] + \[CapitalGamma]];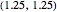

의 위치에 있는 온도 조절 장치가 트리거 신호보다 낮거나 높은 온도를 감지하는 경우 및 이산 변수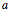가 변화한 경우, 난방기는 켜지거나 꺼지게됩니다.

In[4]:=

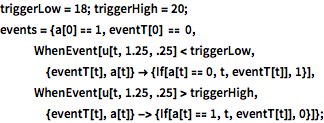
triggerLow = 18; triggerHigh = 20;
events = {a[0] == 1, eventT[0] == 0, 
   WhenEvent[
    u[t, 1.25, .25] < 
     triggerLow, {eventT[t], a[t]} -> {If[a[t] == 0, t, eventT[t]], 
      1}], WhenEvent[
    u[t, 1.25, .25] > 
     triggerHigh, {eventT[t], a[t]} -> {If[a[t] == 1, t, eventT[t]], 
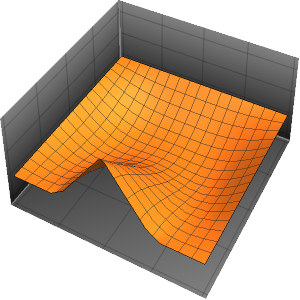
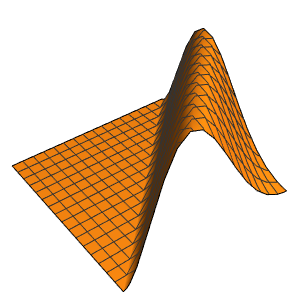
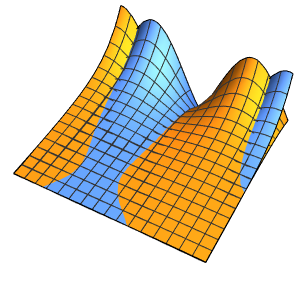
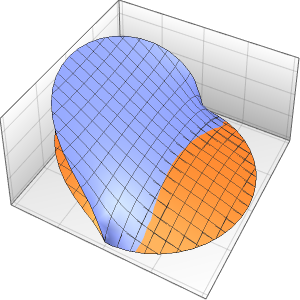
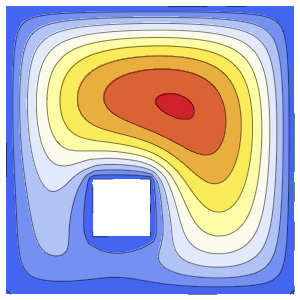
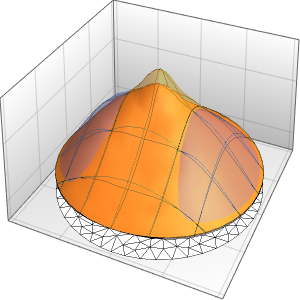
      0}]};

외부 온도와 동일한 초기 조건에서 편미분 방정식의 시간 적분을 관찰합니다.

In[5]:=

eqn = {pde, u[0, x, y] == outsideTemp[0], events};
res = Monitor[
  NDSolveValue[
   eqn, {u, a}, {t, 0, 2*24}, {x, y} \[Element] \[CapitalOmega], 
   DiscreteVariables -> {eventT[t], a[t]}, 
   EvaluationMonitor :> (monitor = Row[{"t = ", CForm[t]}])], monitor]

Out[5]=

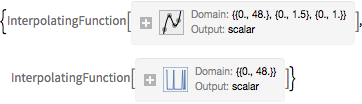
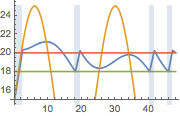
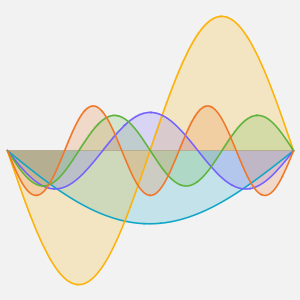
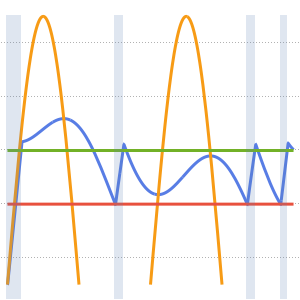
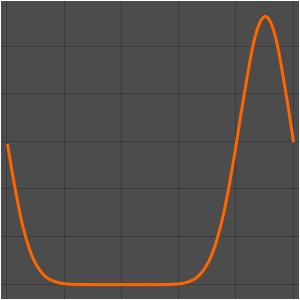
온도 조절 장치에서 측정된 온도, 외부 온도, 난방기의 트리거 신호를 시각화합니다. 난방기가 켜져있는 부분은 푸른 배경색으로 표시되어 있습니다.

In[6]:=

hp = Plot[ 25 res[[2]][t], {t, 0, 2*24}, Filling -> Bottom, 
  PlotStyle -> None]; Show[
 Plot[{res[[1]][t, 1.25, .25], outsideTemp[t], 18, 20}, {t, 0, 
   2*24}], hp]

Out[6]=