영역에서 편미분 방정식의 감도 계산
파동 방정식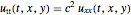 
, 
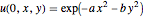의 파라메트릭 의존성을 계산합니다.
파동 방정식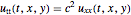 
를 지정합니다.
In[1]:=
eqn = D[u[t, x, y], t, t] == c^2 Laplacian[u[t, x, y], {x, y}];초기 조건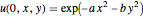 
를 지정합니다.
In[2]:=
ics = {u[0, x, y] == Exp[-((a x)^2 + (b x)^2)],
Derivative[1, 0, 0][u][0, x, y] == 0};일정한 디리클레 경계 조건을 지정합니다.
In[3]:=
bcs = DirichletCondition[u[t, x, y] == 0, True];파라메트릭 함수를 설정합니다.
In[4]:=
pfun = ParametricNDSolveValue[{eqn, ics, bcs},
u, {t, 0, 5}, {x, y} \[Element] Disk[], {a, b, c}];매개 변수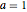 
, 
, 
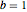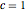에 대한 감도 
,
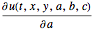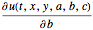, 그리고 
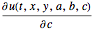를 구합니다.
In[5]:=
ifda = D[pfun[a, 1, 1], a] /. {a -> 1};
ifda = D[pfun[1, b, 1], b] /. {b -> 1};
ifdc = D[pfun[1, 1, c], c] /. {c -> 1};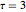
인 
, 
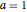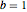, 그리고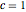 
의 파라메트릭 함수를 플롯하고 감도 
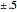의 해에 겹쳐 해당 감도 범위를 시각화합니다.
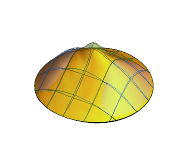
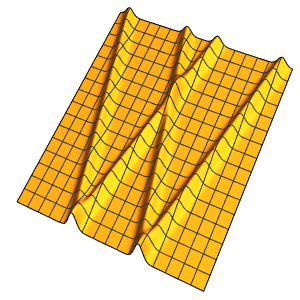
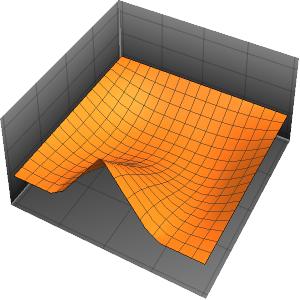
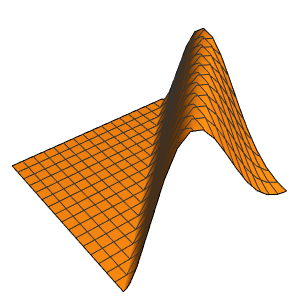
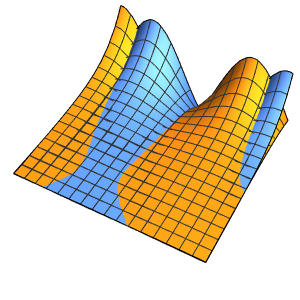
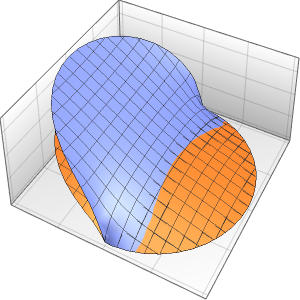
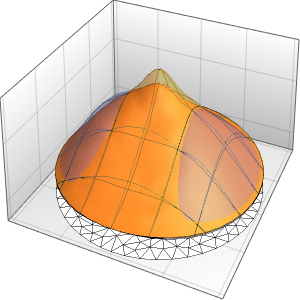
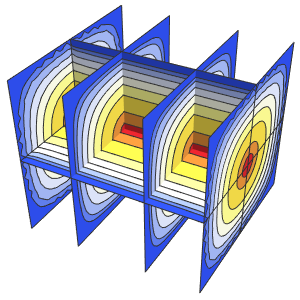
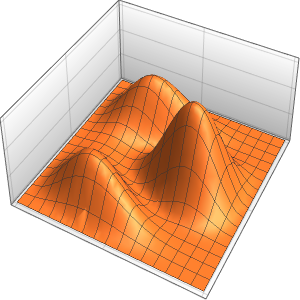
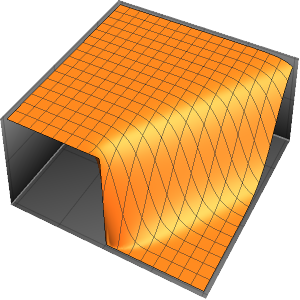
In[6]:=
Plot3D[Evaluate[(pfun[a, b, c][\[Tau], x,
y] + .5 {0, 1, -1} D[pfun[a, b, c][\[Tau], x, y], a]) /. {a ->
1, b -> 1, c -> 1, \[Tau] -> 3}], {x, y} \[Element] Disk[],
PlotRange -> All, Boxed -> False, Axes -> False, Mesh -> 5,
PlotStyle -> {Automatic, Opacity[0.3], Opacity[0.3]}]Out[6]=
