박스의 양자 입자 관찰: Wolfram Language 11의 신기능

박스의 양자 입자 관찰

길이가 xMax 그리고 yMax 측면을 가진 이차원의 직사각형에서 자유롭게 움직이는 양자 입자는 이차원의 시간 의존 슈뢰딩거 방정식 및 경계에서 파동 함수를 강제로 제로로하는 경계 조건에 의해 설명됩니다.

In[1]:=

eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
     Laplacian[\[Psi][x, y, t], {x, y}];

In[2]:=

bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] == 
    0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};

이 방정식은 이른바 고유 상태의 형식적인 무한 합인 일반적인 솔루션을 가집니다.

In[3]:=

DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]

Out[3]=

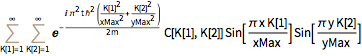
결합된 고유 상태와 동일한 초기 조건을 정의합니다.

In[4]:=

initEigen = \[Psi][x, y, 0] == 
   2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];

이 경우, 해석은 초기 조건 (단위 계수)의 시간 의존 배수와 같습니다.

In[5]:=

DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]

Out[5]=

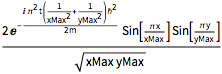
고유 상태의 합인 초기 조건을 정의합니다. 초기 조건은 고유 상태가 아니기 때문에 입자의 위치에 대한 확률 밀도는 시간 의존적이 됩니다.

In[6]:=

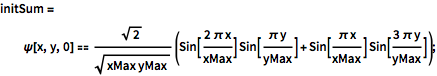
initSum = \[Psi][x, y, 0] == 
   Sqrt[2]/Sqrt[
    xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] + 
      Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);

새로운 초기 조건에서 해결합니다.

In[7]:=

sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]

Out[7]=

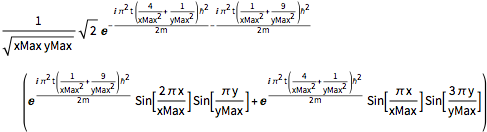
축소된 플랑크 상수, 전자 질량, 원자 크기의 박스에 값을 넣고 전자 질량, 나노 미터, 펨토세컨드의 단위를 사용하여 확률 밀도를 계산합니다.

In[8]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "ElectronMass" * ("Nanometers")^2/"Femtoseconds"]

Out[8]=

In[9]:=

\[Rho][x_, y_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1, 
   xMax -> 1, yMax -> 1}

Out[9]=

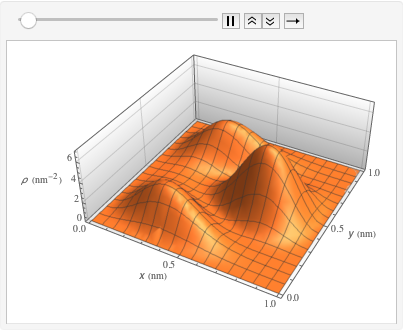
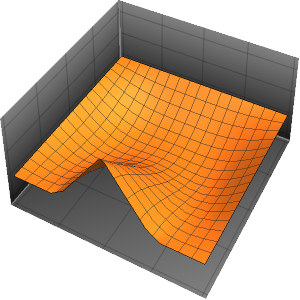
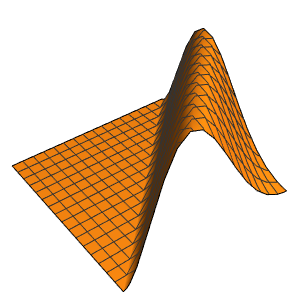
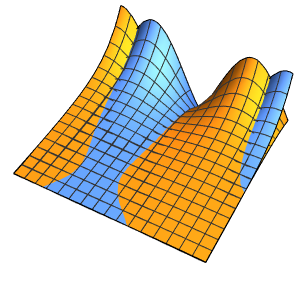
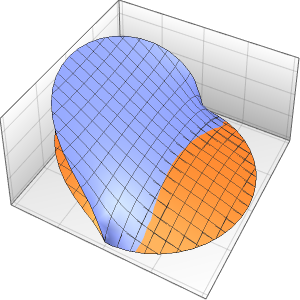
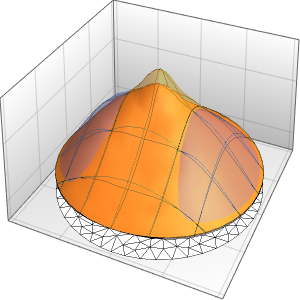
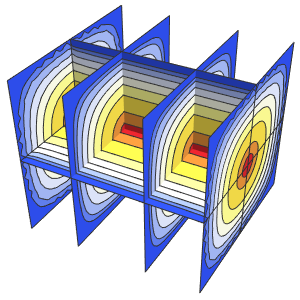
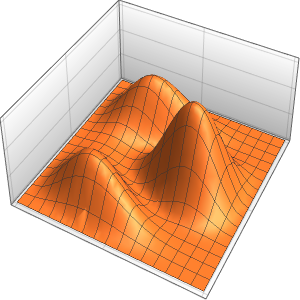
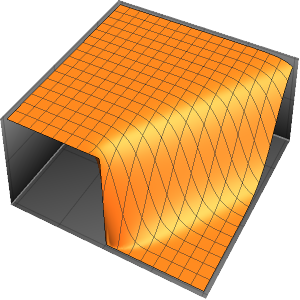
시간 경과에 따른 상자의 확률 밀도를 시각화합니다.

In[10]:=

ListAnimate[
 Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1}, 
   PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0, 
   19, .5}]]