충격파의 형성 조사
점액의 흐름에 대한 버거스 (Burgers) 방정식을 사용하여 충격파의 형성을 조사합니다.
In[1]:=
TraditionalForm[BurgersEquation = \!\(
\*SubscriptBox[\(\[PartialD]\), \({t}\)]\(u[x, t]\)\) + u[x, t] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x}\)]\(u[x,
t]\)\) == \[Epsilon] \!\(
\*SubscriptBox[\(\[PartialD]\), \({x, 2}\)]\(u[x, t]\)\)]Out[1]//TraditionalForm=
구분적인 초기 조건을 규정합니다.
In[2]:=
InitialCondition = u[x, 0] == Piecewise[{{1, x < 0}}]; 초기값 문제를 해결합니다.
In[3]:=
dsol = DSolveValue[{BurgersEquation, InitialCondition},
u[x, t], {x, t}]Out[3]=
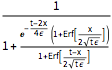
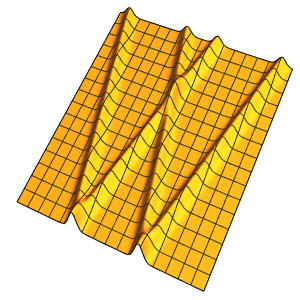
솔루션은 ϵ의 임의의 양의 값에 매끄럽습니다.
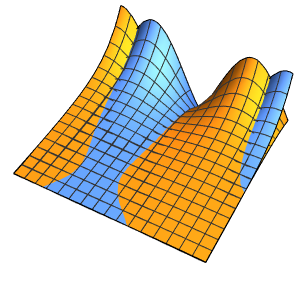
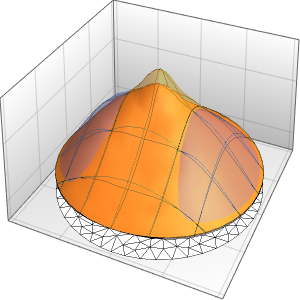
In[4]:=
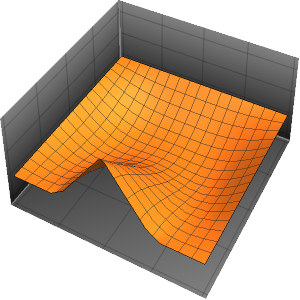
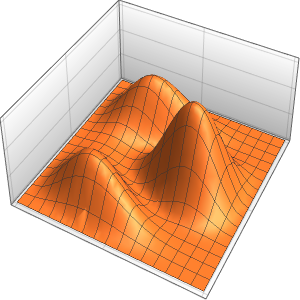
Plot3D[dsol /. {\[Epsilon] -> 1/10}, {x, -2, 2}, {t, 0.001, 5}]Out[4]=
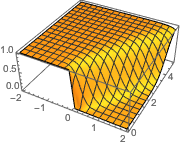
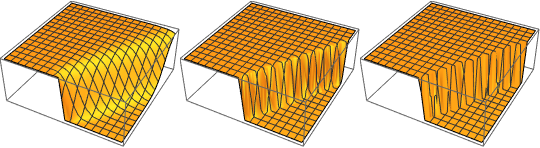
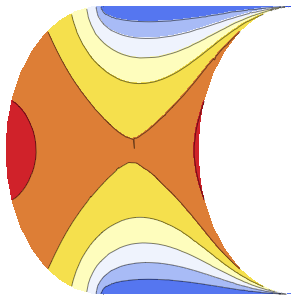
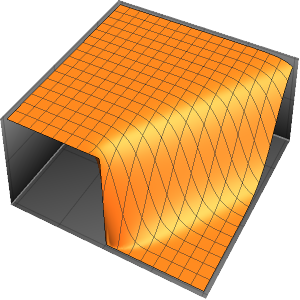
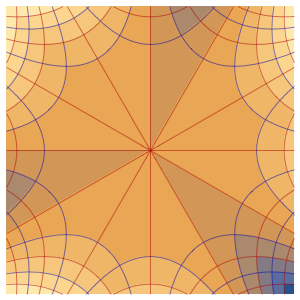
솔루션은 ϵ이 0에 가까워질수록 극한에서 충격의 불연속성을 일으킵니다.
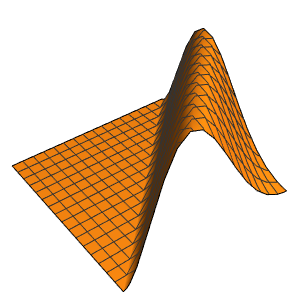
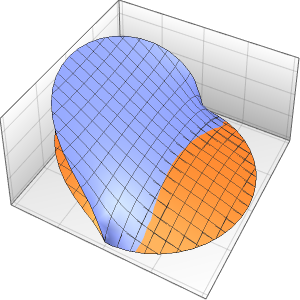
In[5]:=

Row[Table[Plot3D[dsol, {x, -2, 2}, {t, 0.001, 5},
Exclusions -> None, Ticks -> None],
{\[Epsilon], {1/10, 1/100, 1/1000}}]]Out[5]=