Wolfram 언어™

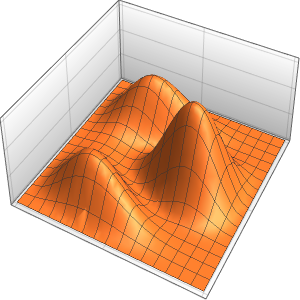
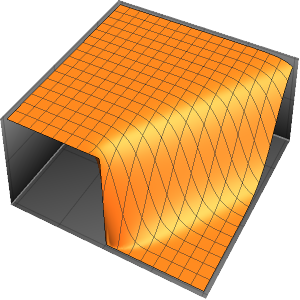
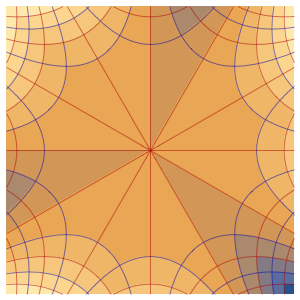
늘려진 실의 진동 조사

파동 방정식을 사용하여 늘린 실의 진동을 조사합니다.

In[1]:=

weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}];

진동 중 실 끝은 고정된 채로 유지되도록 지정합니다.

In[2]:=

bc = {u[0, t] == 0, u[\[Pi], t] == 0};

실의 다양한 위치에서의 초기값을 제공합니다.

In[3]:=

ic = {u[x, 0] == x^2 (\[Pi] - x), \!\(\*SuperscriptBox[\(u\), TagBox[ RowBox[{"(", RowBox[{"0", ",", "1"}], ")"}], Derivative], MultilineFunction->None]\)[x, 0] == 0};

초기 경계값 문제를 해결합니다.

In[4]:=

dsol = DSolve[{weqn, bc, ic}, u, {x, t}] /. {K[1] -> m}

Out[4]=

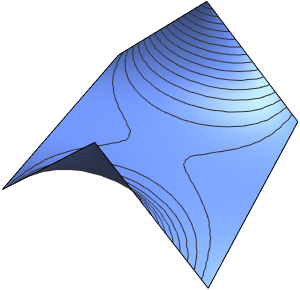
Inactive 합에서 4개의 항을 추출합니다.

In[5]:=

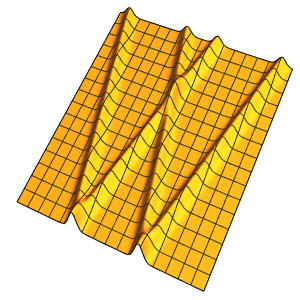
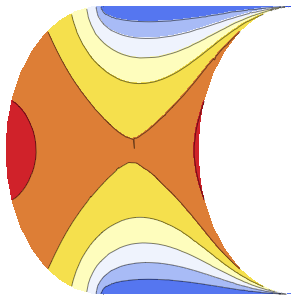
asol[x_, t_] = u[x, t] /. dsol[[1]] /. {\[Infinity] -> 4} // Activate

Out[5]=

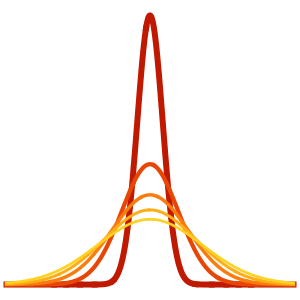
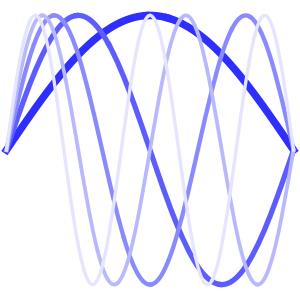
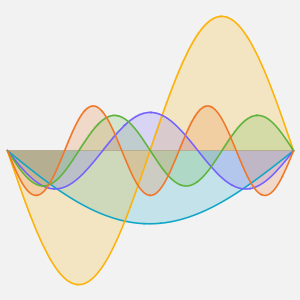
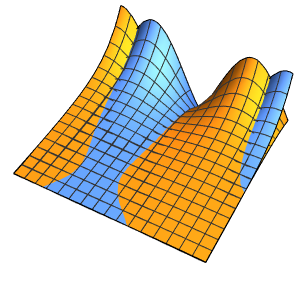
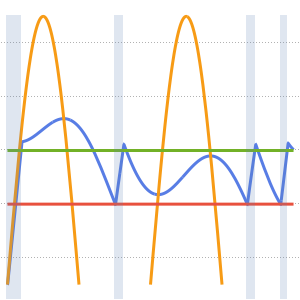
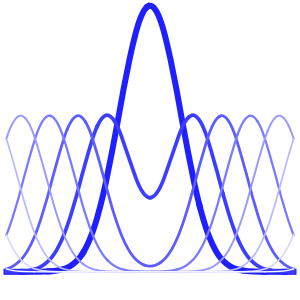
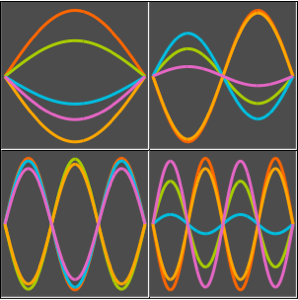
합의 각 항은 정상파를 나타냅니다.

In[6]:=

Table[Show[ Plot[Table[asol[x, t][[m]], {t, 0, 4}] // Evaluate, {x, 0, Pi}, Ticks -> False], ImageSize -> 150], {m, 4}]

Out[6]=

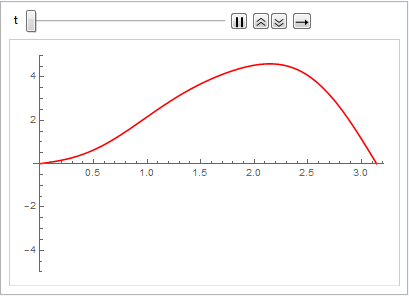
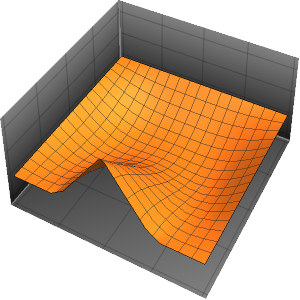
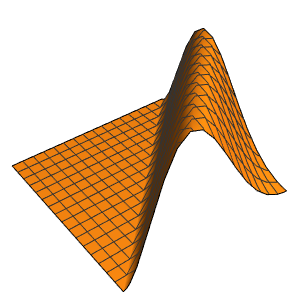
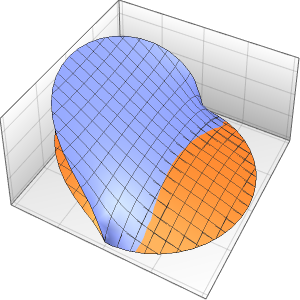
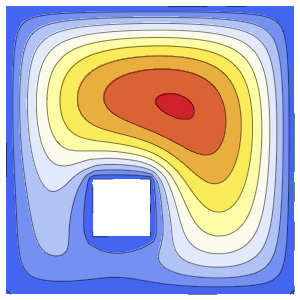
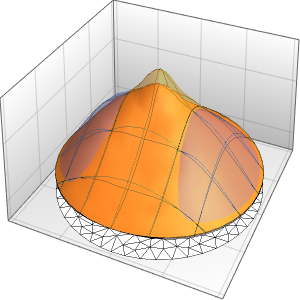
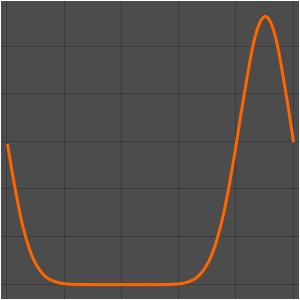
실의 진동을 시각화합니다.

In[7]:=

Animate[Plot[asol[x, t], {x, 0, \[Pi]}, PlotRange -> {-5, 5}, ImageSize -> Medium, PlotStyle -> Red], {t, 0, 2 Pi}, SaveDefinitions -> True]

동영상 작동

동영상 정지