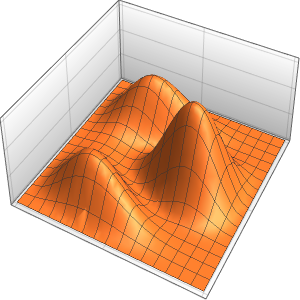
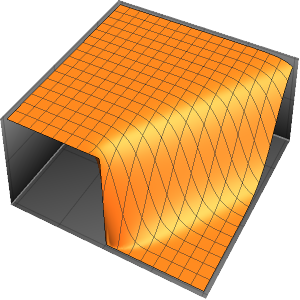
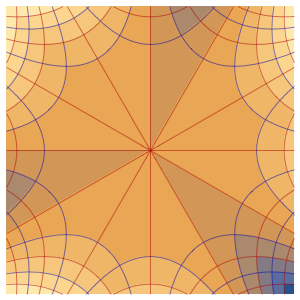
흡수 경계 조건에서 파동 방정식의 해
흡수 경계 조건에서 1차원 파동 방정식을 풉니다.
흡수 경계 조건에서 파동 방정식을 지정합니다. 노이만 값은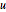 
의 첫 번째 시간 도함수를 위한 것임을 주의합니다.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];파동 방정식의 초기 조건을 지정합니다.
In[2]:=
u0[x_] := Evaluate[D[0.125 Erf[(x - 0.5)/0.125], x]];
ic = {u[0, x] == u0[x], Derivative[1, 0][u][0, x] == 0};유한 요소법을 사용하여 방정식을 풉니다.
In[3]:=
ufun = NDSolveValue[{eqn, ic}, u, {t, 0, 1}, {x, 0, 1},
Method -> {"MethodOfLines",
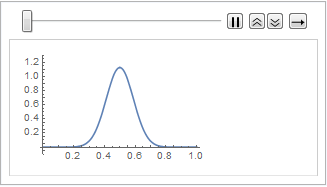
"SpatialDiscretization" -> {"FiniteElement"}}];흡수 경계 조건에서 파동 방정식을 시각화합니다.
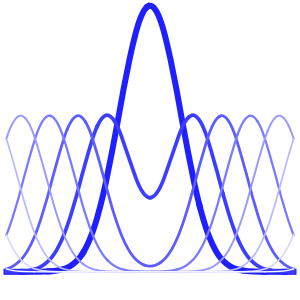
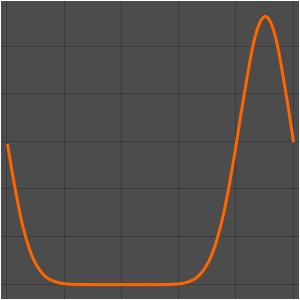
In[4]:=
list = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0, 1,
0.1}];
ListAnimate[list]
