원형막의 진동 생성: Wolfram Language 11의 신기능

‹›

원형막의 진동 생성

이차원의 파동 방정식을 사용하여 반경 1의 원형막 진동을 모델링합니다.

In[1]:=

eqn = r D[u[r, t], {t, 2}] == D[r D[u[r, t], r], r];

막의 경계가 고정되어 있도록 지정합니다.

In[2]:=

bc = u[1, t] == 0;

문제의 초기 조건을 지정합니다.

In[3]:=

ic = {u[r, 0] == 0, Derivative[0, 1][u][r, 0] == 1};

DSolve를 사용하여 베셀 함수에 대한 솔루션을 얻습니다.

In[4]:=

(dsol = DSolve[{eqn, bc, ic}, u[r, t], {r, t}]) // TraditionalForm

Out[4]//TraditionalForm=

Inactive의 합에서 유한수의 항을 추출합니다.

In[5]:=

h[r_, t_] = 
  u[r, t] /. dsol[[1]] /. {\[Infinity] -> 3} // Activate // N;

최소 모드는 약 2.612의 주기를 갖습니다.

In[6]:=

N[(2 \[Pi])/BesselJZero[0, 1]]

Out[6]=

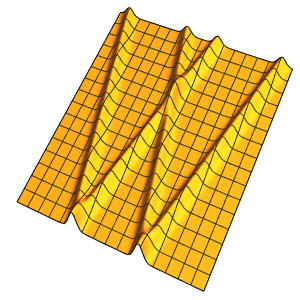
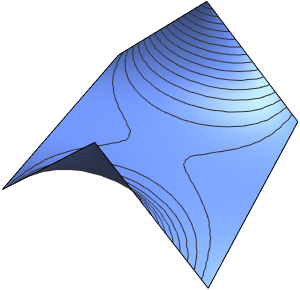
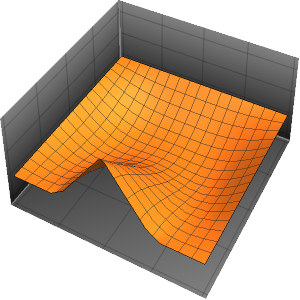
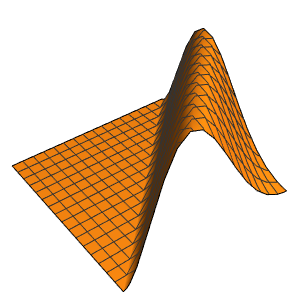
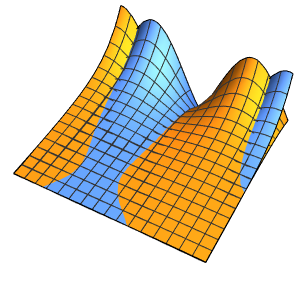
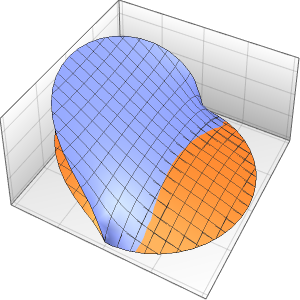
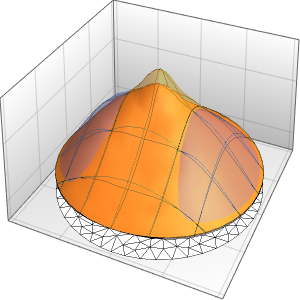
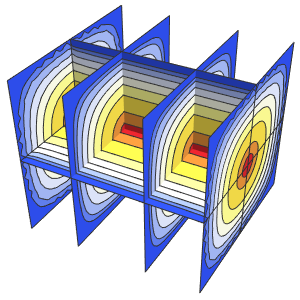
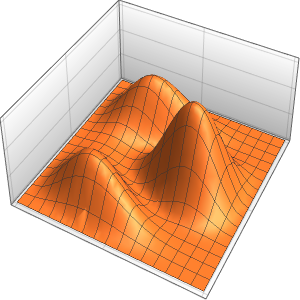
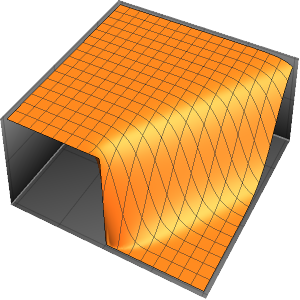
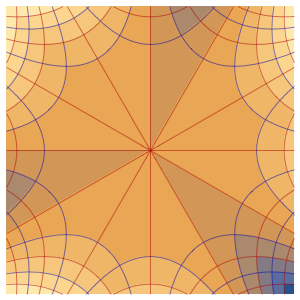
4주기에 걸친 막의 진동을 시각화합니다.

In[7]:=

ListAnimate[
 Table[Plot3D[
   Evaluate[h[r, t] /. {r -> Sqrt[x^2 + y^2]}], {x, y} \[Element] 
    Disk[], PlotRange -> {-1, 1}, Ticks -> None, Mesh -> True, 
   MeshStyle -> {Red, Blue}, PlotStyle -> Yellow, Boxed -> False, 
   Axes -> False, ImageSize -> Medium, AspectRatio -> 1, 
   Background -> Lighter[Orange, 0.85]], {t, 0, 10.45, 0.05}]]