유럽형 콜 옵션값 구하기: Wolfram Language 11의 신기능

유럽형 콜 옵션값 구하기

기초 자산 가격과 행사 가격 가치 모두가 $100일때, 비위험 이자율이 6%, 기초 자산의 변동성이 20%, 만기가 1년인 경우 유럽형 바닐라 콜 옵션의 값을 블랙-숄즈 모델을 사용하여 구합니다.

In[1]:=

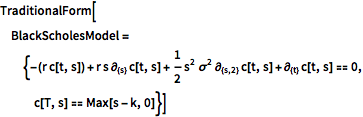
TraditionalForm[BlackScholesModel = {-(r c[t, s]) + r s \!\(
\*SubscriptBox[\(\[PartialD]\), \({s}\)]\(c[t, s]\)\) + 
     1/2 s^2 \[Sigma]^2 \!\(
\*SubscriptBox[\(\[PartialD]\), \({s, 2}\)]\(c[t, s]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \({t}\)]\(c[t, s]\)\) == 0, 
   c[T, s] == Max[s - k, 0]}]

Out[1]//TraditionalForm=

경계값 문제를 해결합니다.

In[2]:=

(dsol = c[t, s] /. 
    DSolve[BlackScholesModel, c[t, s], {t, s}][[
     1]]) // TraditionalForm

Out[2]//TraditionalForm=

유럽형 바닐라 옵션값을 계산합니다.

In[3]:=

dsol /. {t -> 0, s -> 100, k -> 100, \[Sigma] -> 0.2, T -> 1, 
  r -> 0.06}

Out[3]=

FinancialDerivative에서 주어진 값과 비교합니다.

In[4]:=

FinancialDerivative[{"European", "Call"}, {"StrikePrice" -> 100.00, 
  "Expiration" -> 1},  {"InterestRate" -> 0.06, "Volatility" -> 0.2 , 
  "CurrentPrice" -> 100}]

Out[4]=