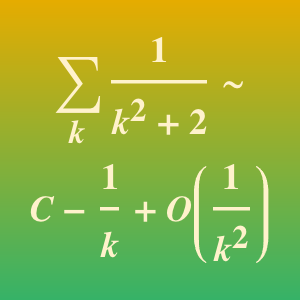境界層常微分方程式を解く(AsymptoticDSolveValue)
この例では,摂動パラメータ [e]が0に設定されると次数が減少する線形微分方程式の摂動問題を考える.この方程式の次数は,摂動パラメータ 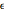 が0に設定されると減少する.パラメータを小さい値に固定すると,解の性質は
が0に設定されると減少する.パラメータを小さい値に固定すると,解の性質は 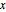 と
と 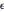 の相対スケールに依存し,解は左端点0(
の相対スケールに依存し,解は左端点0(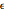 が
が 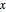 よりかなり大きい)付近の境界層と,右端点1(
よりかなり大きい)付近の境界層と,右端点1( が
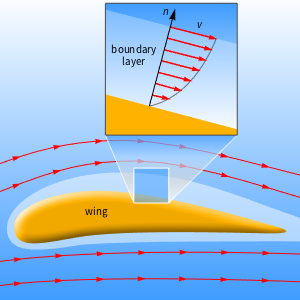
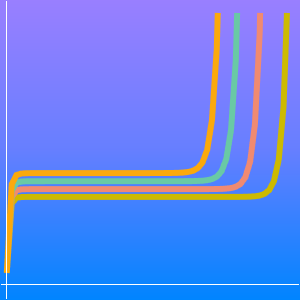
が 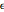 よりかなり大きい)付近の外部領域で構成されるものとみなすことができる.このような問題は特異摂動問題または境界層問題という.
よりかなり大きい)付近の外部領域で構成されるものとみなすことができる.このような問題は特異摂動問題または境界層問題という.
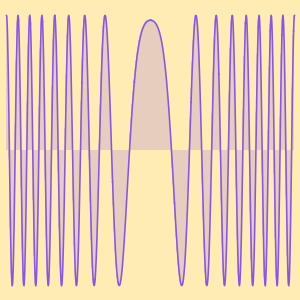
境界層問題について主要項のWKB近似を求める.
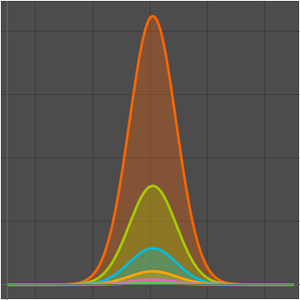
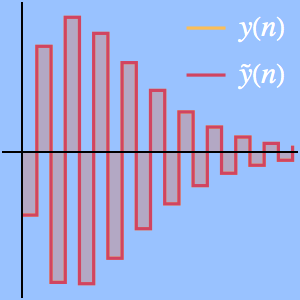
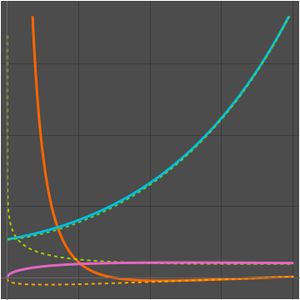
厳密解と比較する.
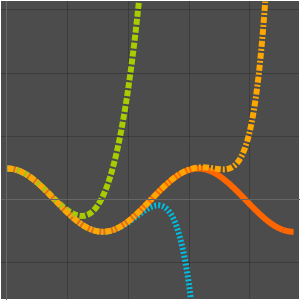
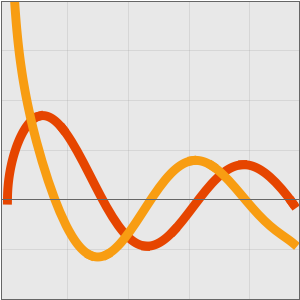
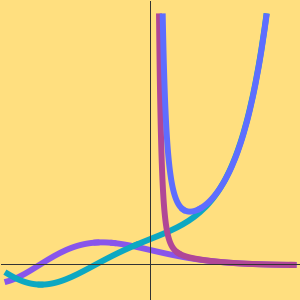
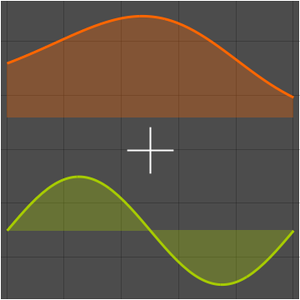
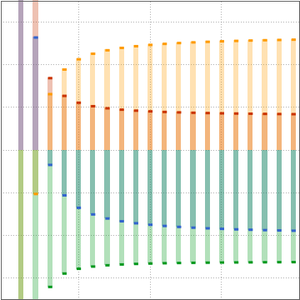
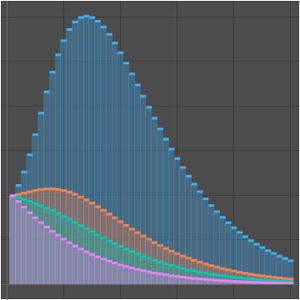
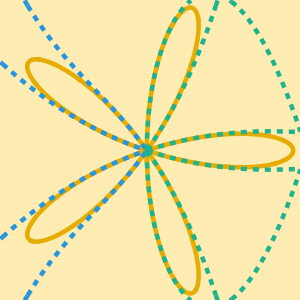
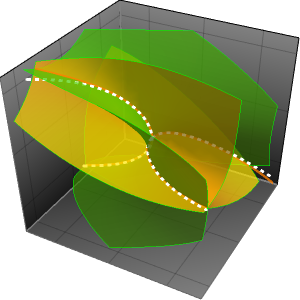
解と近似をプロットする.