Mathematica 8 brinda una suite completa de funcionalidades incorporadas para realizar análisis, diseño y simulación de sistemas de control de tiempo continuo y discreto con técnicas tanto clásicas como modernas. El poderoso motor de computación simbólico-numérica de Mathematica facilita el uso de soluciones analíticas para estudiar relaciones entre elementos de diseño y ofrece información muy valiosa sobre la conducta de sistemas de control complejos. Con capacidades numéricas de todo tipo de precisión, selección automática de algoritmos y visualizaciones avanzadas, Mathematica 8 es ideal para construir y analizar sistemas de control, documentar decisiones de diseño y probar controladores interactivamente: todo desde una plataforma única.

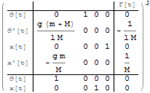
• Funciones para construir modelos de espacio de estado y de función de transferencia en forma natural y simple conversión de una forma a la otra.
• Construcción de modelos linearizados de modelo de espacio de estado de sistemas descritos por ecuaciones diferenciales o en diferencia.
• Conversión entre modelos de tiempo continuo y tiempo discreto usando una selección amplia de algoritmos.
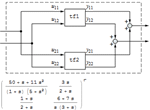
• Conexiones y manipulaciones de modelo, como selección o eliminación de subpartes, diseño de un set de sistemas en cascada, construcción de interconexiones de subsistemas, etc.
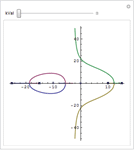
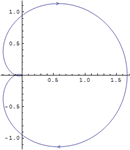
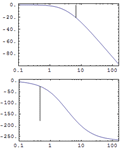
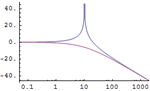
• Colección de herramientas de respuesta de frecuencias como diagrama de Bode, diagrama de Nyquiest, diagrama de Nichols y diagrama de valor singular para ayudar en el análisis y diseño de sistemas.
• Capacidad de analizar modelos de espacio de estado y conversión entre realizaciones distintas, incluyendo formas de Kalman, Jordan, equilibradas y otras.
• Amplia selección de algoritmo de diseño de retroalimentación como robusta asignación de polos y control lineal cuadrático óptimo para mejorar el rendimiento del sistema.
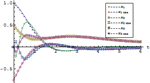
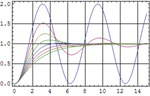
• Funciones de simulación para determinar respuestas de estado y de salida de sistemas de lazo cerrado y abierto.
• Capacidad incorporada para resolver ecuaciones de Riccati y de Lyapunov.

Especifique modelos de sistemas lineales, invariables en el tiempo en forma natural »	Conecte dos sistemas en paralelo »	Analice la conducta de sistemas interactivamente »
Determine estabilidad de sistemas usando funciones incorporadas »	Visualice la estabilidad relativa de sistemas »	Estudie la respuesta de frecuencia de sistemas multivariables »
Construya reguladores y observadores para sistemas »	Simule la respuesta de modelos de espacio de estado de función de transferencia »	Construya un filtro de Kalman para un sistema estocástico »

FUNCIONES RELACIONADAS

TransferFunctionModel  StateSpaceModel  ToContinuousTimeModel  ToDiscreteTimeModel  SystemsModelSeriesConnect  SystemsModelExtract  SystemsModelFeedbackConnect  SystemsModelDelete  RootLocusPlot  BodePlot  NyquistPlot  NicholsPlot  SingularValuePlot  GainPhaseMargins  ControllabilityMatrix  ObservabilityMatrix  JordanModelDecomposition  InternallyBalancedDecomposition  StateFeedbackGains  LQEstimatorGains  DiscreteLQRegulatorGains  KalmanEstimator  StateResponse  OutputResponse