Mathematica 8 使用经典的和现代的技术为连续和离散时间控制系统提供一套分析、设计和仿真的扩展的内置功能。Mathematica 强大的符号数值引擎使得使用分析解来学习设计与洞察复杂控制系统间的关系变得容易。具有任意精度的数值、自动算法选择以及高级可视化功能，Mathematica 8 是一个理想的工具，用于构建和分析控制系统、记载设计决策以及用交互式的方法测试控制器，而所有这些均可在一个单一的平台中完成。

• 构建自然形式的状态空间模型和传递函数模型的函数，且不同形式之间易于互相转换。
• 构建由微分和差分方程描述的系统的线性状态空间模型。
• 使用广范围选择的算法在连续时间和离散时间模型间进行转换。
• 模拟连接和操控，例如选择或删除子部件、级联系统、构建子系统的互联等。
• 包括波特图、奈奎斯特图、尼科尔斯图以及奇异值图在内的频响工具，以辅助系统分析和设计 。
• 可以分析状态空间模型以及处理不同实现间的转换，包括卡尔曼、约旦、平衡和其他格式。
• 广泛的反馈设计算法例如鲁棒式极点分配和线性二次优化控制，以提高系统的性能。
• 仿真函数决定开环和闭环系统的状态和输出响应。
• 内置求解 Riccati 和 Lyapunov 方程组的能力。

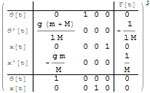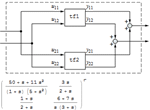以自然的格式指定线性、时不变系统的模型 »	并行连接两个系统 »	交互式分析系统行为 »
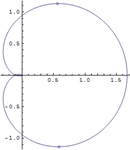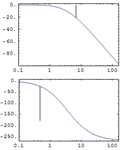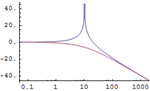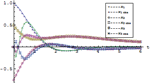
使用内置函数决定系统稳定性 »	可视化系统的相对稳定性 »	研究多变量系统的频率响应 »
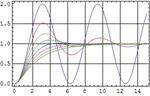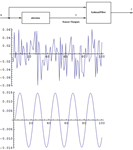构建系统的调节器和观测器 »	状态空间和传递函数模型的仿真  »	构建随机系统的卡尔曼滤波器 »

相关函数

TransferFunctionModel  StateSpaceModel  ToContinuousTimeModel  ToDiscreteTimeModel  SystemsModelSeriesConnect  SystemsModelExtract  SystemsModelFeedbackConnect  SystemsModelDelete  RootLocusPlot  BodePlot  NyquistPlot  NicholsPlot  SingularValuePlot  GainPhaseMargins  ControllabilityMatrix  ObservabilityMatrix  JordanModelDecomposition  InternallyBalancedDecomposition  StateFeedbackGains  LQEstimatorGains  DiscreteLQRegulatorGains  KalmanEstimator  StateResponse  OutputResponse