Mathematica 8は，古典的な技法と最新の技法を使って連続時間制御系および離散時間制御系の解析，設計，シミュレーションを実行するための包括的な組込み機能を提供する．Mathematica のパワフルな記号および数値計算エンジンにより，設計要素間の関係を調べるための解析的解法の使用が簡単になり，複合制御系の動作への貴重な洞察が得られる．任意精度数計算，アルゴリズムの自動選択，高度な可視化機能を備えた Mathematica 8は，制御系の構築と解析，設計決定の文書化，コントローラのインタラクティブな検証がすべて一つで実行できる，理想的なプラットフォームである．

• 状態空間モデルおよび伝達関数モデルを自然形式で構築するための関数を備え，一つの形式から別の形式への変換も簡単
• 微分方程式または差分方程式で記述される系の線形状態空間モデルの構築
• さまざまなアルゴリズムを使った，連続時間モデルと離散時間モデルの間の変換
• 部分的な選択や削除，一連の系のカスケード接続，下位の系の相互接続の構築等のモデルの接続および操作
• 制御系の解析および設計で役立つボード線図，ナイキスト線図，ニコルス線図，特異値プロット等の周波数応答ツールのコレクション
• 状態空間モデルを解析し，カルマン，ジョルダン，平衡，その他の形式を含むさまざまな実現間の変換を行う機能
• 制御系の性能を向上させるロバスト極配置や線形二次形式最適制御等の多岐に渡るフィードバック設計アルゴリズム
• 開ループ制御系および閉ループ制御系の状態と出力応答を求めるシミュレーション関数
• リッカチ方程式およびリャプノフ方程式を解くための組込み機能

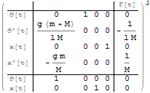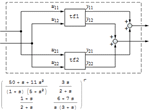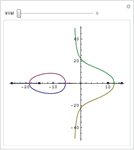線形時不変系を自然な形式で指定する »	2つの系を並列接続する »	系の動作をインタラクティブに解析する »
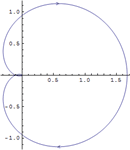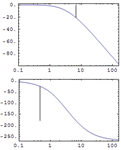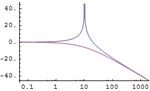組込み関数を使って系の安定性を調べる »	系の相対安定性を可視化する »	多変量の系の周波数応答を調べる »
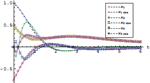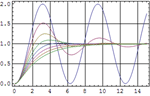系の制御器と観測器を構築する »	空間状態モデルまたは伝達関数モデルの応答をシミュレーションする »	確率系のためにカルマン(Kalman)フィルタを構築する »

関連関数

TransferFunctionModel  StateSpaceModel  ToContinuousTimeModel  ToDiscreteTimeModel  SystemsModelSeriesConnect  SystemsModelExtract  SystemsModelFeedbackConnect  SystemsModelDelete  RootLocusPlot  BodePlot  NyquistPlot  NicholsPlot  SingularValuePlot  GainPhaseMargins  ControllabilityMatrix  ObservabilityMatrix  JordanModelDecomposition  InternallyBalancedDecomposition  StateFeedbackGains  LQEstimatorGains  DiscreteLQRegulatorGains  KalmanEstimator  StateResponse  OutputResponse