Mathematica 8은 고전적 기법 및 최신 기술을 사용하여 연속, 비연속 시간 제어 시스템의 분석, 설계, 시뮬레이션을 실행할 수 있는 포괄적인 기능을 광범위하게 내장하고 있습니다. Mathematica 의 강력한 기호 및 수치 연산 엔진은 설계 요소 간의 관계를 조사하기위한 분석적인 해법의 사용이 용이하여, 복잡한 제어 시스템의 동작 이해에 대한 귀중한 통찰력 제공에 도움을 줍니다. 정밀한 수치 연산, 자동 알고리즘 선택법 그리고 고급 수준의 시각화 기능을 가진, Mathematica 8은 제어 시스템의 구축 및 분석, 설계 결정을 위한 문서작업 그리고 인터랙티브한 제어기 검증 등의 모든 작업을 하나의 플랫폼에서 할 수 있는 이상적인 도구입니다.

• 상태-공간 모델 및 이동 함수 모델 설계를 위한 기본형 및 손쉬운 함수 형식 변환
• 미분 또는 차등 방정식으로 나타낸 시스템의 선형화된 상태-공간 모델 구축
• 다양한 알고리즘을 사용하여 연속 및 비연속 시간 모델 사이의 변환
• 서브파트의 선택 및 삭제, 시스템 셋 정렬, 서브시스템의 상호 접속 설계와 같은 연결 및 조작에 대한 모델링
• 시스템 제어 및 설계를 위한 보드 선도, Nyquist 선도, Nichols 선도 그리고 특이치 선도와 같은 주파수 응답 관련 도구
• 고정-상태 모델 분석과 칼만, 조르단, 균형 그리고 그 외 다른 형식을 포함한 다양한 인식 간의 전환 능력
• 시스템 성능 향상을 위한 활발한 pole-assignmen과 LQ(linear-quadratic) 최적 제어와 같은 피드백 설계 디자인에 대한 폭넓은 선택
• 개루프 제어 시스템 및 폐루프 제어계의 상태 및 출력 반응 결정을 위한 시뮬레이션 함수
• Riccati 및 Lyapunov 방정식 풀이 기능 내장

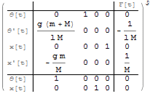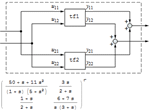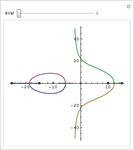선형, 시간 불변 시스템의 자연형 모델링 »	두 시스템의 병렬 연결 »	시스템 형태의 인터랙티브한 분석 »
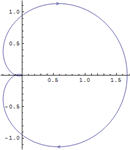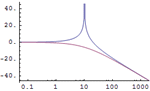내장 함수를 이용한 시스템 안정성 확인 »	시스템의 비교 안정도 시각화 »	다변수 시스템의 주파수 응답 연구 »
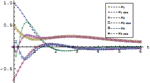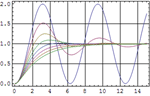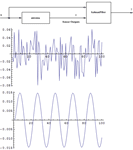시스템을 위한 제어기 및 관측기 구축 »	상태 공간 모델 및 전달 함수 모델의 반응 »	Stochastic 시스템에 대한 Kalman 필터 구축 »

관련 기능

TransferFunctionModel  StateSpaceModel  ToContinuousTimeModel  ToDiscreteTimeModel  SystemsModelSeriesConnect  SystemsModelExtract  SystemsModelFeedbackConnect  SystemsModelDelete  RootLocusPlot  BodePlot  NyquistPlot  NicholsPlot  SingularValuePlot  GainPhaseMargins  ControllabilityMatrix  ObservabilityMatrix  JordanModelDecomposition  InternallyBalancedDecomposition  StateFeedbackGains  LQEstimatorGains  DiscreteLQRegulatorGains  KalmanEstimator  StateResponse  OutputResponse