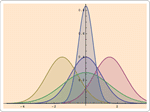
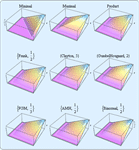
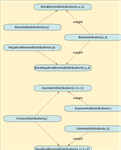
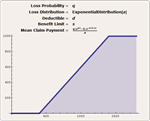
Mathematica 8 在分布模型中引入了重要的革新理念。第一个是非参数分布，非参数方法的自动化与推广可以用于指定分布属性的计算。第二是导出分布，通过函数转换、截断或混合等从现有分布中创建。第三是由公式例如概率密度函数、累积分布函数或生存函数定义的分布。由于我们提供了各种不同的分布类型，因此建模和分析架构的创建具有前所未有的灵活性与易用性。

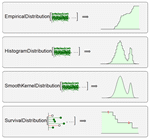
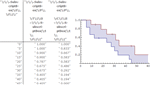
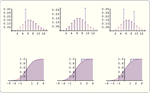
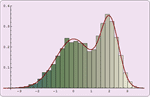
• 非参数分布包括经验分布、直方图分布、平滑核分布等。 »
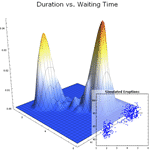
• 具有自动固定或自适应带宽选择的核密度估计。 »
• 优化的单变量和多变量经验分布。 »
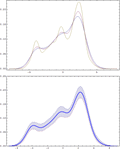
• 用于删失数据的非参数最大似然估计。 »
• 利用删截和删失分布进行有效的生存和可靠性建模。 »
• 包括转换、截断、混合等分布在内的导出分布。 »
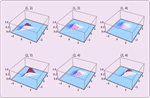
• 随机变量的单变量和多变量转换。 »
• 来自于任何分布的次序统计量的单元和联合分布。 »
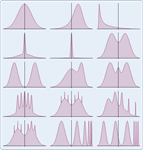
• 具有任意分量分布的分量混合分布。 »
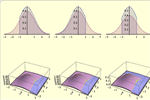
• 具有离散和连续加权分布的参数混合分布。 »
• 任意维数、连续和离散的截断分布。 »
• 任意维数、连续和离散的删截分布。 »
• 用于多核系列和任意边缘分布的 Copula 分布。 »
• 来自于任意高维分布的任意维数的边缘分布。 »
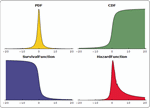
• 定义于概率密度函数、累积密度函数或生存函数的公式分布。 »

直接从数据创建分布 »	使用非参数分布像使用其他参数一样简单 »	计算30多个非参数分布属性的任一个 »
利用任意维数的非参数数据模型 »	估计多变量非参数概率和期望 »	分析左、右、区间删截数据 »
使用非参数分布模拟自然过程 »	创建关于非参数密度估计的置信包络 »	求解密度估计的最优化问题 »
使用导出分布从现有分布中创建新的分布 »	截断一个分布 »	在正态分布上进行仿射变换 »
对分布应用删截 »	创建联合次序分布 »	边缘分布的视图 »
准备特殊变换的表格 »	产生混合分布的图形集 »	使用不同的 Copula 核 »
特殊参数混合的图 »	仿真一个导出分布 »	可视化乘积分布的等概率密度级别 »
比较非参数和参数可靠性模型 »	在先进的混合模型中利用非参数分布 »	创建分层参数混合模型 »
研究一个自定义概率分布的属性 »	模拟保险的索赔支付 »	创建您自己的分布 »

相关函数

EmpiricalDistribution  HistogramDistribution  SmoothKernelDistribution  SurvivalDistribution  KernelMixtureDistribution  ProbabilityDistribution  TransformedDistribution  OrderDistribution  MixtureDistribution  ParameterMixtureDistribution  TruncatedDistribution  CensoredDistribution  CopulaDistribution  ProductDistribution  MarginalDistribution