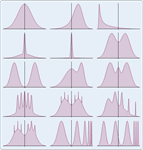
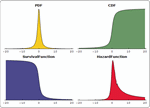
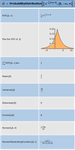
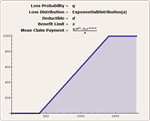
Mathematica 8은 분포 모델링에 있어서 근본적으로 새로운 아이디어들을 소개하고 있습니다. 구체적인 분포 특성 연산을 위해 사용되는 모든 범위의 비모수 메소드를 자동화한 비모수 분포가 그 첫번째 입니다. 두번째는 공식, 변환, 절단, 혼합 등의 기존 분포로부터 만들어지는 파생된 분포입니다. 세번째는 PDF, CDF, 생존 함수와 같은 분포로 정의되는 공식들입니다. 여러 모양의 분포들은 대게 같이 구동하여 모델링 제작, 프레임 워크 분석에 전례없이 융통성있고 쉽게 사용할 수 있습니다.

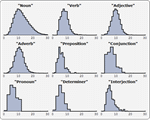
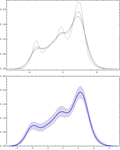
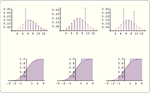
• 경험 분포, 히스토그램, 평활화 커널 포함하는 비모수 분포 »
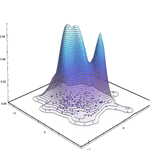
• 자동화된 고정 또는 적응 너비 선택으로 핵 밀도 추정 »
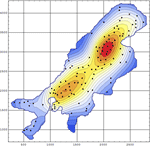
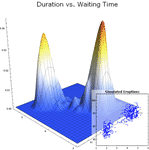
• 최적화된 일변량 그리고 다변량 경험 분포 »
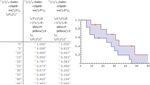
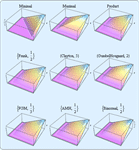
• 중도 절단 데이터를 위한 비모수 최대 우도 추정 »
• 절단 및 중도 절단된 분포로 효과적인 생존 및 신뢰도 모델링 »
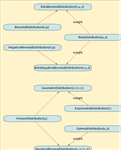
• 변환, 절단, 혼합 등을 포함하는 파생 분포 »
• 난수 값의 일변량 및 다변량 변환 »
• 일변량 및 모든 분포로부터의 통계값의 공동 분포 »
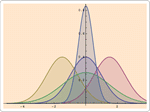
• 임의 요소 분포를 가지는 혼합 요소 분포 »
• 이산 및 연속 무게 분포를 가지는 모수 혼합 분포 »
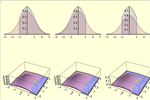
• 차원에 상관없이 연속 및 이산적 절단 분포 »
• 차원에 상관없이 연속 및 이산적 중심 절단 분포 »
• 다중 핵 요소들과 모든 주변 분포의 코플라 분포 »
• 차원에 상관없이 고차원 분포로부터의 주변 분포 »
• PDF, CDF 또는 생존 함수의 공식으로 부터 정의되는 분포 »

데이터로부터 직접 분포 설정 »	다른 분포와 비슷한 비모수 분포 사용 »	30 이상의 비모수 분포 특성 연산 »
차원에 상관없이 비모수 데이터 모델링 »	다변량 비모수 확률과 기대값 추정 »	좌, 우, 구간 중도 절단 데이터 분석 »
시뮬레이션에 이용되는 자연적 과정 비모수 분포 »	비모수 밀도 추정에 대한 신뢰 구간 작성 »	밀도 추정에서의 최적화  »
파생 분포를 이용하여 기존 분포로부터 새로운 분포 만들기 »	절단 분포 »	정규 분포에서의 아핀 변환  »
분포에 중심절단 적용 »	결합 차수 분포  »	주변 분포 시각화 »
특수 변환들에 대한 도표 »	혼합 분포  »	다른 코플라 핵 이용 »
특수 모수 혼합 그래프 »	파생 분포 시뮬레이션 »	곱 분포를 위한 등위 확률 밀도 레벨에 대한 시각화 »
비모수와 모수 신외성 모델 비교 »	정교한 혼합 모델에서의 비모수 분포  »	계층적 모수 혼합 모델 »
사용자 확률 분포의 특성 »	보험에 대한 보험금 모델링 »	사용자 분포 작성 »

관련 기능

EmpiricalDistribution  HistogramDistribution  SmoothKernelDistribution  SurvivalDistribution  KernelMixtureDistribution  ProbabilityDistribution  TransformedDistribution  OrderDistribution  MixtureDistribution  ParameterMixtureDistribution  TruncatedDistribution  CensoredDistribution  CopulaDistribution  ProductDistribution  MarginalDistribution