Wolfram 언어™

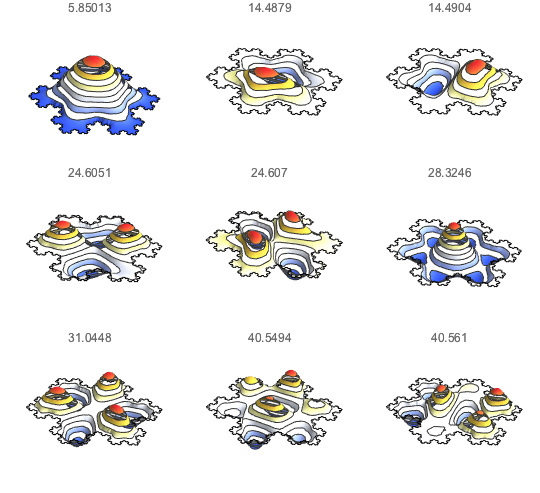
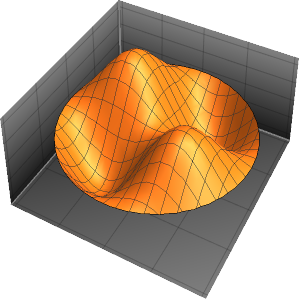
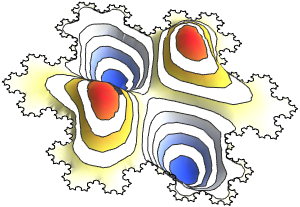
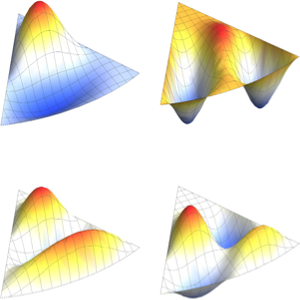
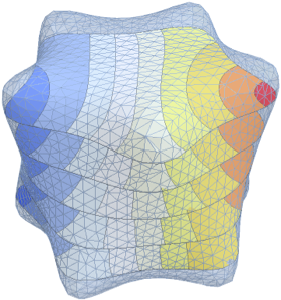
코크 (Koch) 눈송이의 스펙트럼 계산

재귀적인 코크 눈송이를 생성합니다.

In[1]:=

KochStep[{p1_, p2_}] := With[{q1 = p1 + (p2 - p1)/3, q3 = p1 + 2 (p2 - p1)/3, q2 = (p1 + (p2 - p1)/3) + RotationMatrix[-\[Pi]/3].(p2 - p1)/3}, {p1, q1, q2, q3, p2}]; KochStep[pp : {{_, _} ..}] := Join[Partition[Flatten[Most /@ (KochStep /@ Partition[pp, 2, 1])], 2], {pp[[-1]]}]; vertices = Nest[KochStep, N[{{3 Sqrt[3]/4, 3/4}, {-3 Sqrt[3]/4, 3/4}, {0, -3/2}, {3 Sqrt[3]/4, 3/4}}], 4]; region = Polygon[vertices];

라플라스 연산자를 지정합니다.

In[2]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

디리클레 경계 조건을 지정합니다.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

라플라스 연산자 9개의 고유값과 고유 함수를 계산합니다.

In[4]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] region, 9];

고유값을 조사합니다.

In[5]:=

vals

Out[5]=

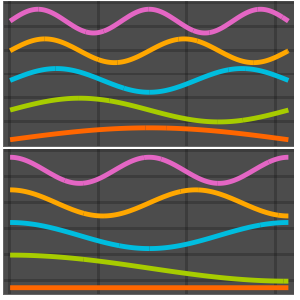
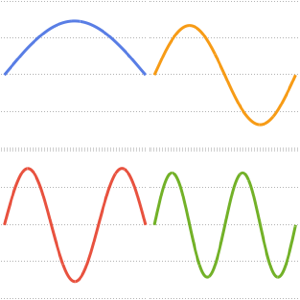
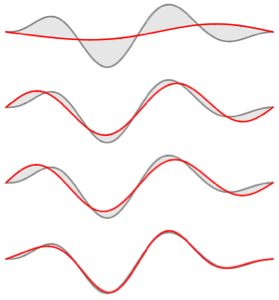
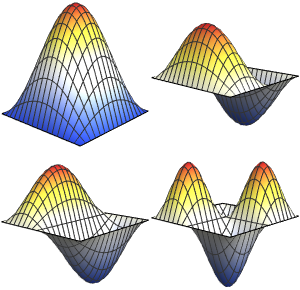
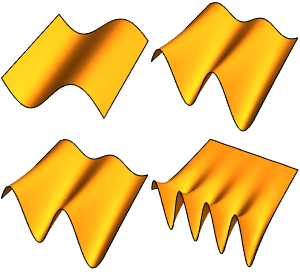
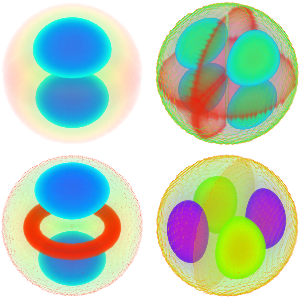
고유 함수를 시각화합니다.

In[6]:=

Grid[Partition[ Table[Plot3D[funs[[i]], {x, y} \[Element] region, PlotLabel -> vals[[i]], MeshFunctions -> {#3 &}, MeshShading -> {Automatic, None}, Mesh -> 10, Background -> None, Boxed -> False, Axes -> None, PlotRange -> All, ColorFunction -> "TemperatureMap"], {i, Length[vals]}], 3], Spacings -> 0]

Out[6]=