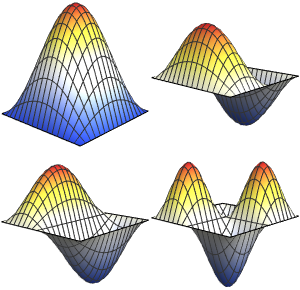
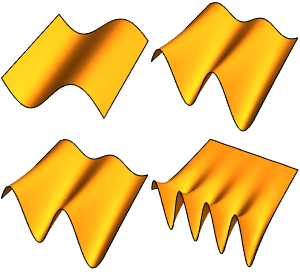
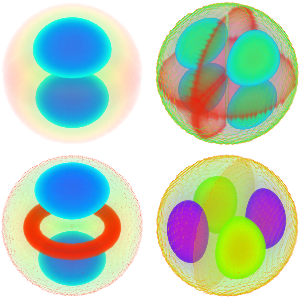
고유 함수 전개의 생성
구간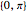 
에서 디리클레 조건을 가지는 함수 
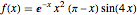를 1D 라플라시안에서 제공하는 기본에 대한 고유 함수 전개를 계산합니다.
In[1]:=
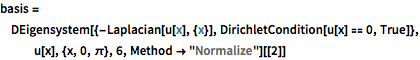
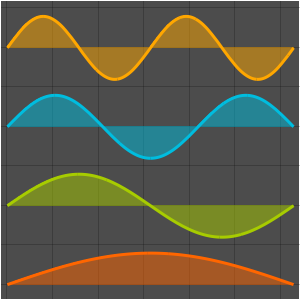
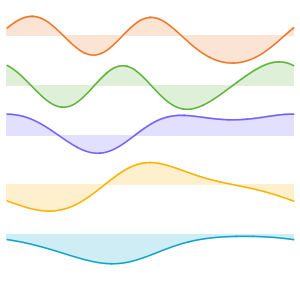
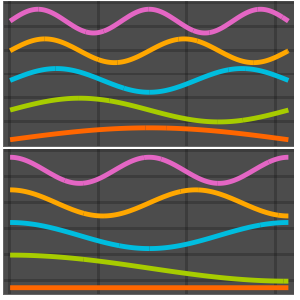
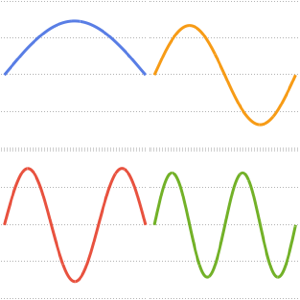
basis = DEigensystem[{-Laplacian[u[x], {x}],
DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6,
Method -> "Normalize"][[2]]Out[1]=
함수 f[x]에 대한 푸리에 계수를 계산합니다.
In[2]:=
f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]In[3]:=
coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] //
FullSimplify);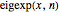
을 전개의 
차 부분합으로 정의합니다.
In[4]:=
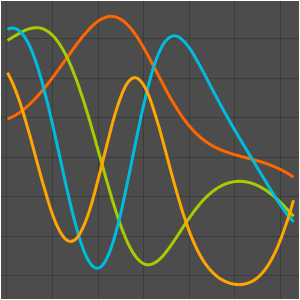
eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]In[5]:=
eigexp[x, 3] // NOut[5]=
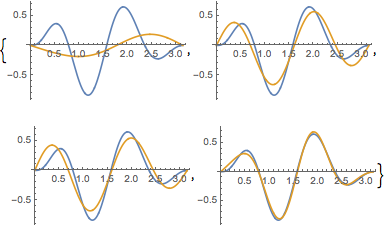
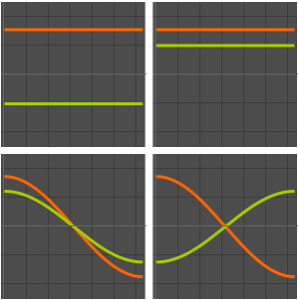
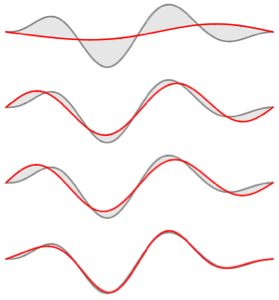
이 함수와 다른 n 값의 경우 고유 함수 전개를 비교합니다.
In[6]:=
Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]Out[6]=
