원환면의 라플라스 방정식 조사

디리클레 제약 조건을 가진 정방 원환면의 가장 작은 5개의 고유값과 고유 함수의 라플라스 방정식을 구합니다.

한변의 길이가 1인 정사각형에서 주기적 경계 조건을 지정합니다.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

근원점의 값을 지정합니다. 주기적인 조건으로, 이것은 정사각형의 다른 세개의 코너의 값이 되기도 해야합니다.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

고유값과 고유 함수를 계산합니다.

In[3]:=

{vals, funs} = NDEigensystem[ Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

고유값을 확인합니다.

In[4]:=

vals

Out[4]=

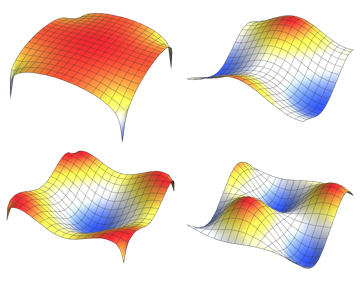
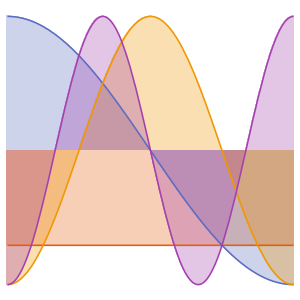
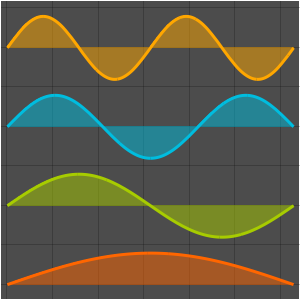
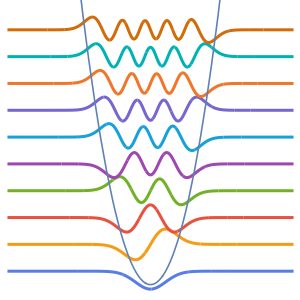
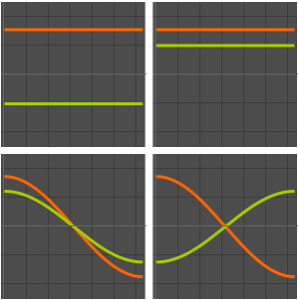
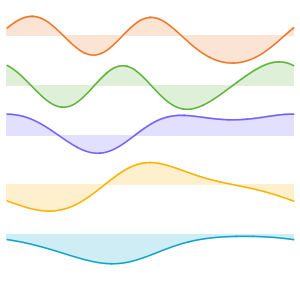
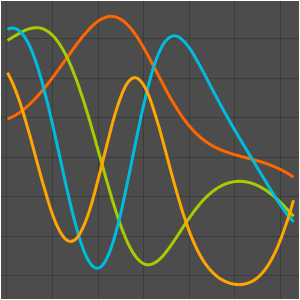
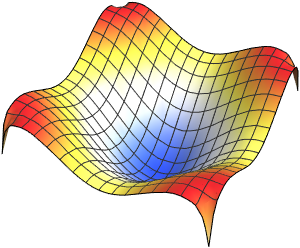
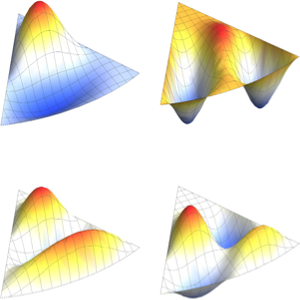
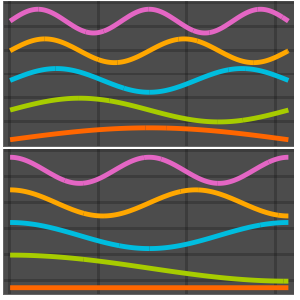
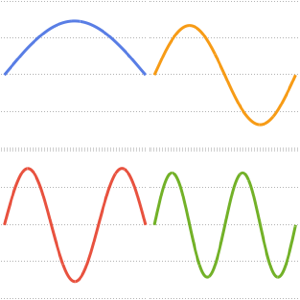
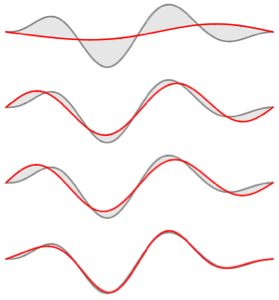
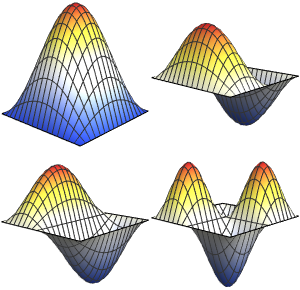
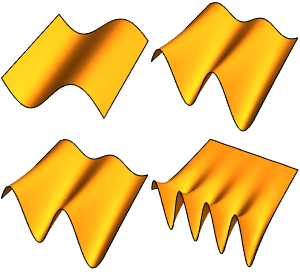
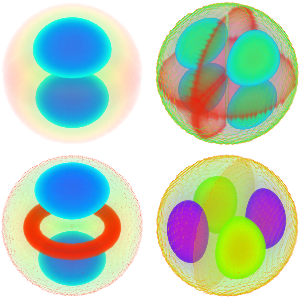
고유 함수를 시각화합니다.

In[5]:=

ImageCollage[ Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ funs, Background -> Transparent]

Out[5]=