Wolfram 언어™

비대칭 잠재력을 가진 스튀름-리우빌 연산자 분석

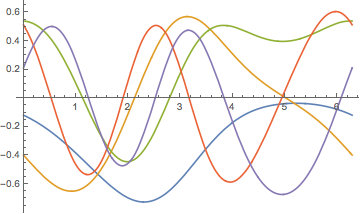
스튀름-리우빌 연산자의 가장 작은 5개의 주기적인 고유값과 고유 함수를 구합니다.

스튀름-리우빌 연산자를 지정합니다.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

주기적인 경계 조건을 지정합니다.

In[2]:=

\[ScriptCapitalB] = u[0] == u[2 \[Pi]];

가장 작은 5개의 고유치와 고유 함수를 구합니다.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

고유값을 확인합니다.

In[4]:=

vals

Out[4]=

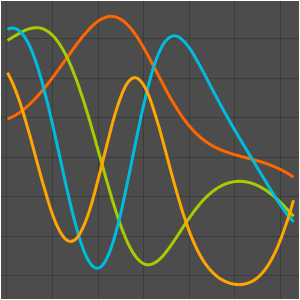
고유 함수를 시각화합니다.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=