Wolfram 언어™

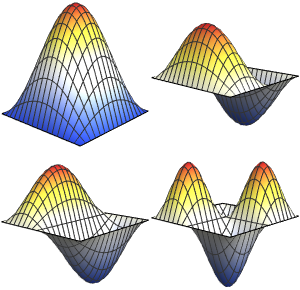
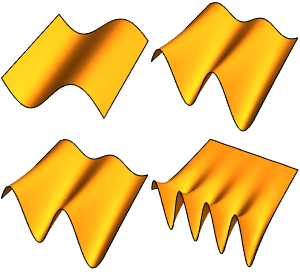
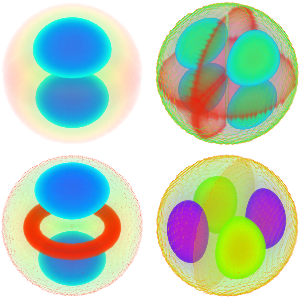
파동 연산자의 고유 문제 조사

일차원 공간에서 일반화된 파동 방정식 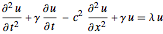의 가장 작은 4개의 고유값과 고유 함수를 구합니다.

일반화된 파동 연산자 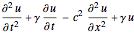를 설정합니다.

In[1]:=

\[Gamma] = 1.3; c = 1.1; op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] - c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];

일차원 영역에서 가장 작은 4개의 고유값과 고유 함수를 구합니다.

In[2]:=

{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];

고유값을 확인합니다.

In[3]:=

vals

Out[3]=

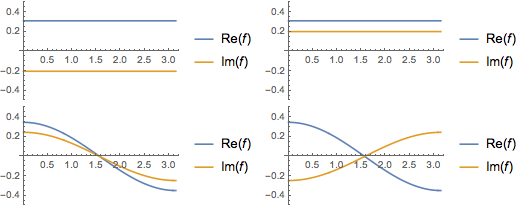
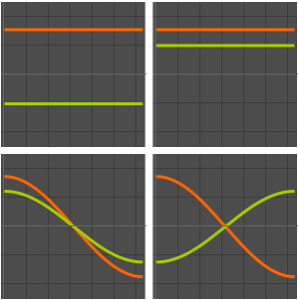
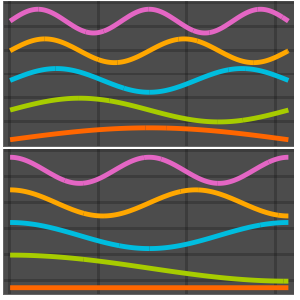
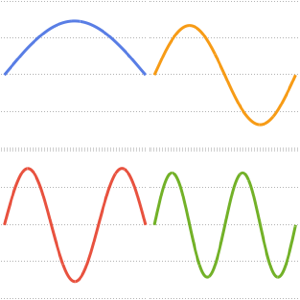
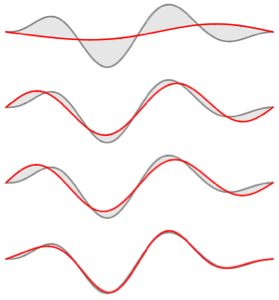
고유 함수의 실수와 허수 부분을 시각화합니다. 고유 함수는 고유 값과 같이 공역 시키는 짝이 있는 점에 유념합니다.

In[4]:=

Grid[Partition[ Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5, PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]

Out[4]=