구간의 고유값 구하기: Wolfram Language 11의 신기능

구간의 고유값 구하기

영역을 지정합니다.

In[1]:=

\[CapitalOmega] = 
  ImplicitRegion[(x^2 + y^2 + 2 y)^2 < 4 (x^2 + y^2), {x, y}];

라플라스 연산자를 지정합니다.

In[2]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

디리클레 경계 조건을 지정합니다.

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

미세한 메쉬에서 구간의 고유값과 고유 함수를 찾습니다.

In[4]:=

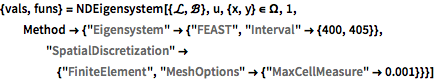
{vals, funs} = 
 NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, 
  u, {x, y} \[Element] \[CapitalOmega], 1, 
  Method -> {"Eigensystem" -> {"FEAST", "Interval" -> {400, 405}}, 
    "SpatialDiscretization" -> {"FiniteElement", 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.001}}}]

Out[4]=

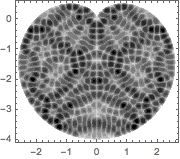
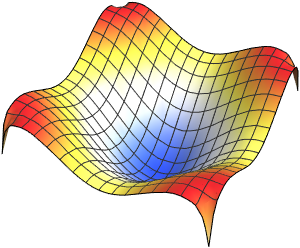
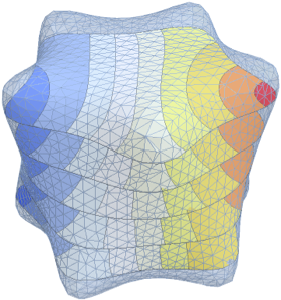
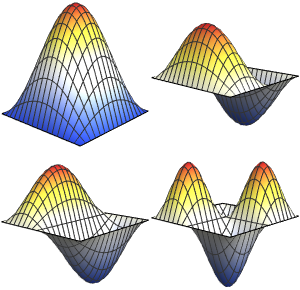
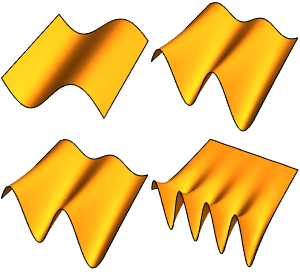
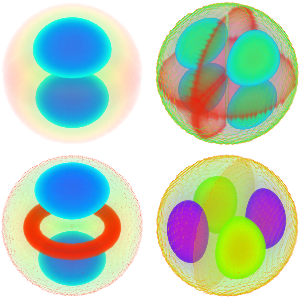
나타난 고유 함수를 시각화합니다.

전체 Wolfram 언어 입력 표시하기

In[5]:=

ContourPlot[
 Evaluate[Abs[funs[[1]][x, y]]^(1/2)], {x, y} \[Element] 
  funs[[1]]["ElementMesh"], PlotPoints -> 200, 
 ColorFunction -> (GrayLevel[1 - #] &), AspectRatio -> Automatic, 
 ContourStyle -> None, PlotRange -> All, MaxRecursion -> 0]

Out[5]=