아로노프-봄 고유값 구하기
아로노프-봄 효과는 대전된 입자가 전자기 게이지 잠재력의 영향을 받는 동시에 영역내의 자기장이 제로가되는 양자 역학 현상입니다. 이 예에서는 입자의 영역에 수직인 선에 조밀한 자기장을 가진 슈뢰딩거 방정식을 고려하였습니다.
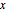 축 중심으로하는
축 중심으로하는 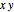 평면 부채형으로 영역을 지정합니다.
평면 부채형으로 영역을 지정합니다.
In[1]:=
\[CapitalOmega] = Disk[{0, 0}, 1, {-\[Pi]/8, \[Pi]/8}];아로노프-봄 연산자를 지정합니다. 자기장은 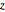 축에 제한됩니다.
축에 제한됩니다.
In[2]:=
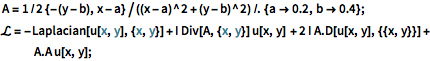
A = 1/2 {-(y - b), x - a}/((x - a)^2 + (y - b)^2) /. {a -> 0.2,
b -> 0.4};
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}] +
I Div[A, {x, y}] u[x, y] + 2 I A.D[u[x, y], {{x, y}}] +
A.A u[x, y];경계 전체에 대한 디리클레 경계 조건을 지정합니다.
In[3]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];6개의 연산자 고유값과 고유 함수를 계산합니다.
In[4]:=
{vals, funs} =
NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y], {x, y} \[Element] \[CapitalOmega], 6]; 고유값을 조사합니다.
In[5]:=
valsOut[5]=
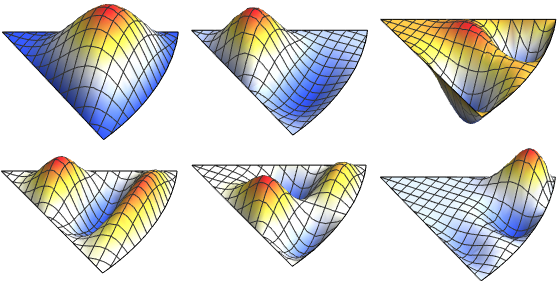
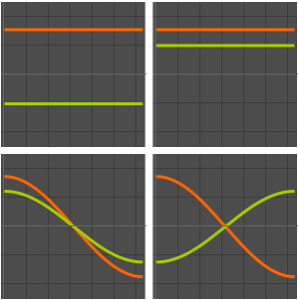
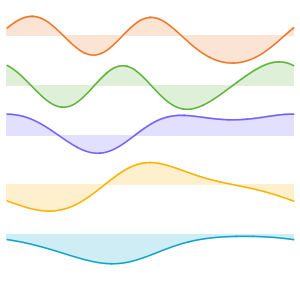
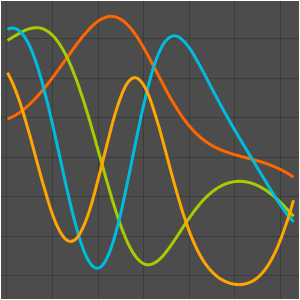
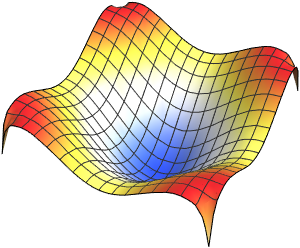
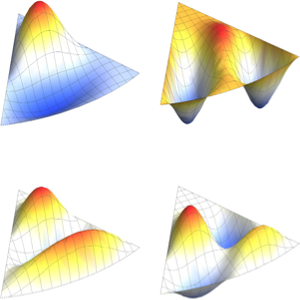
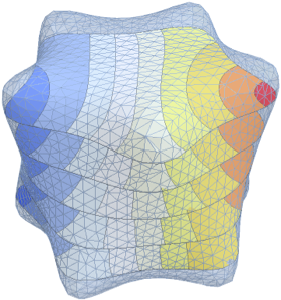
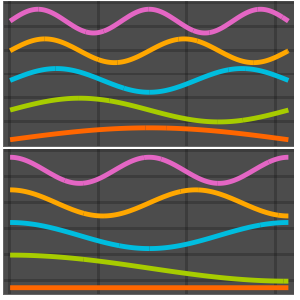
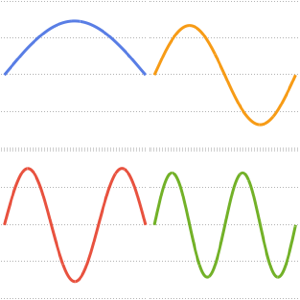
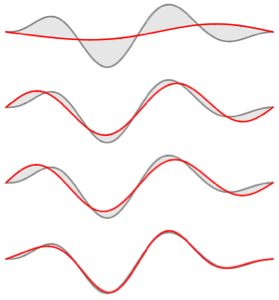
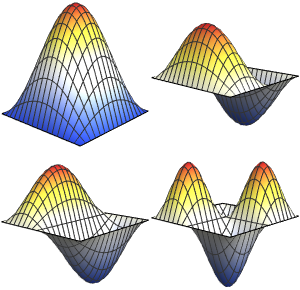
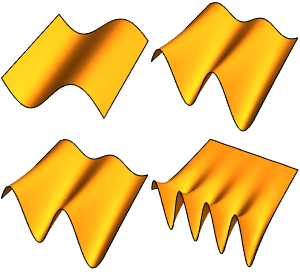
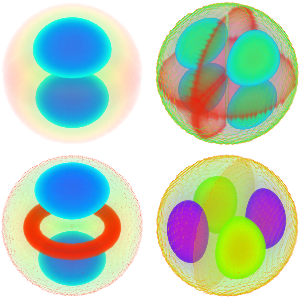
고유 함수의 실부를 시각화합니다.
전체 Wolfram 언어 입력 표시하기
Out[6]=