Wolfram Language™

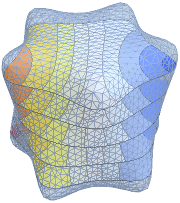
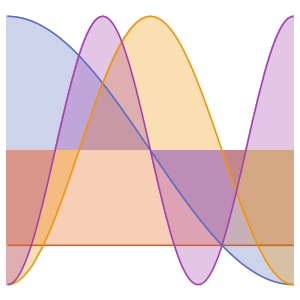
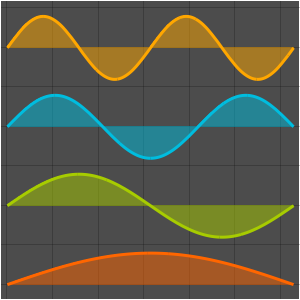
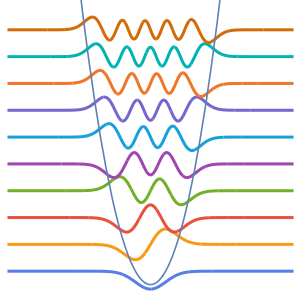
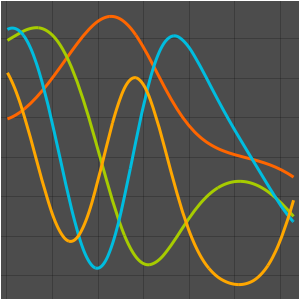
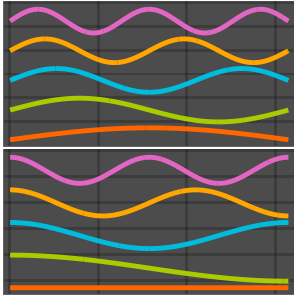
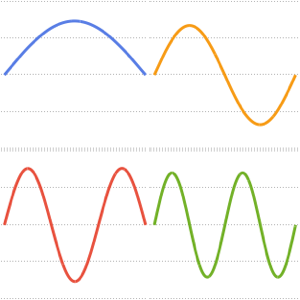
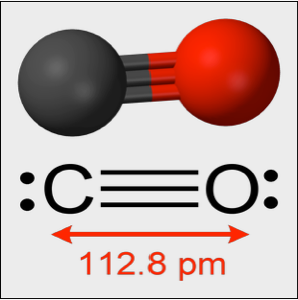
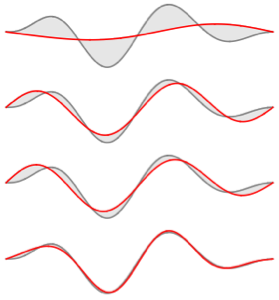
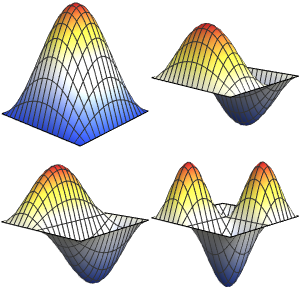
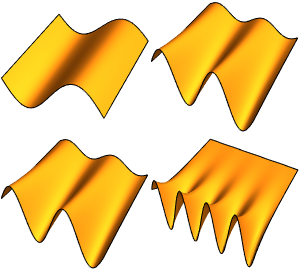
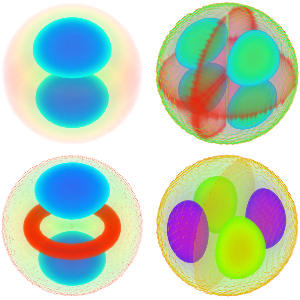
Eigenfunktionen eines 3D Laplace-Operators

Spezifizieren Sie eine 3D-Region.

In[1]:=

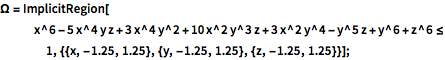
\[CapitalOmega] = ImplicitRegion[ x^6 - 5 x^4 y z + 3 x^4 y^2 + 10 x^2 y^3 z + 3 x^2 y^4 - y^5 z + y^6 + z^6 <= 1, {{x, -1.25, 1.25}, {y, -1.25, 1.25}, {z, -1.25, 1.25}}];

Berechnen Sie die Eigenwerte und Eigenfunktionen des Laplace-Operators.

In[2]:=

{vals, funs} = NDEigensystem[Laplacian[u[x, y, z], {x, y, z}], u, {x, y, z} \[Element] \[CapitalOmega], 4];

Untersuchen Sie die Eigenwerte.

In[3]:=

vals

Out[3]=

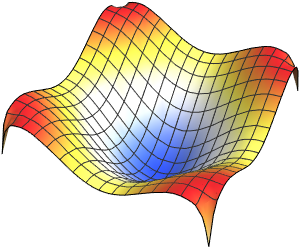
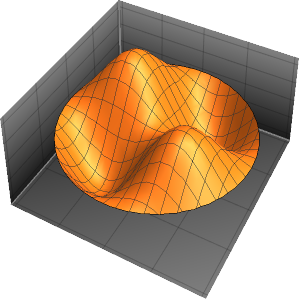
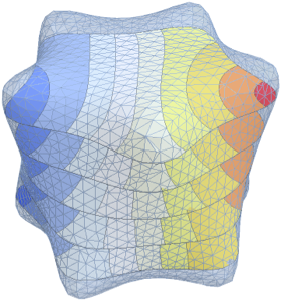
Visualisieren Sie die vierte Eigenfunktion.

In[4]:=

Show[ HighlightMesh[BoundaryDiscretizeRegion[\[CapitalOmega]], Style[2, Opacity[0.3]]], SliceContourPlot3D[ funs[[4]][x, y, z], {"ZStackedPlanes", 5}, {x, y, z} \[Element] \[CapitalOmega], Boxed -> False, Axes -> None, ColorFunction -> "TemperatureMap"]]

Out[4]=