Eine Laplace-Gleichung auf einem Torus untersuchen: Neu in Wolfram Language 11

Eine Laplace-Gleichung auf einem Torus untersuchen

Ermitteln Sie die fünf kleinsten Eigenwerte und Eigenfunktionen einer Laplace-Gleichung auf einem quadratischen Torus mit einer Dirichlet-Randbedingung.

Spezifizieren Sie die periodischen Randbedingungen auf einem Quadrat der Länge 1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Spezifizieren Sie einen Wert am Ursprung. Laut der periodischen Bedingungen muss dies auch der Wert an den anderen drei Ecken des Quadrats sein.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Berechnen Sie die Eigenwerte und Eigenfunktionen.

In[3]:=

{vals, funs} = 
  NDEigensystem[
   Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], 
   u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Untersuchen Sie die Eigenwerte.

In[4]:=

vals

Out[4]=

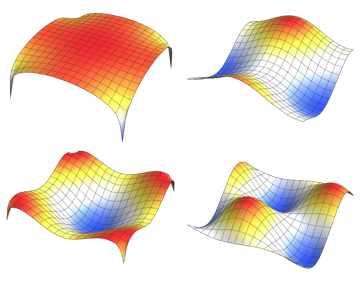
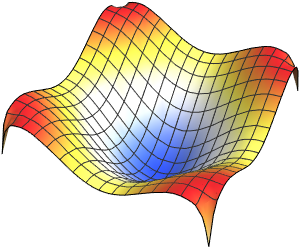
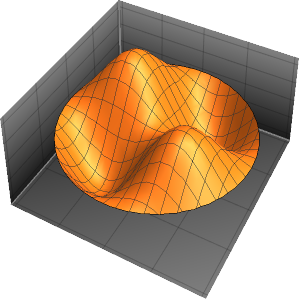
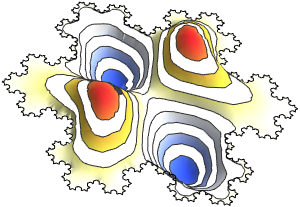
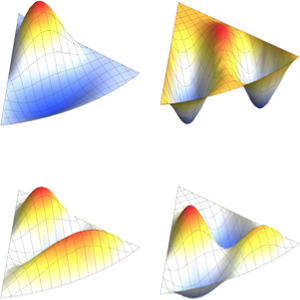
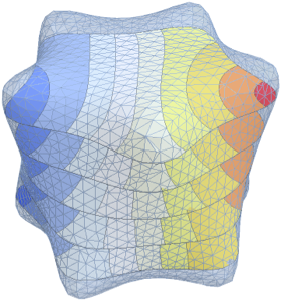
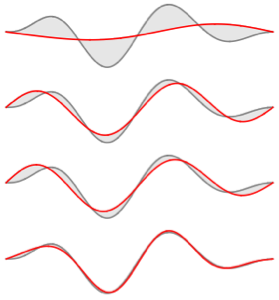
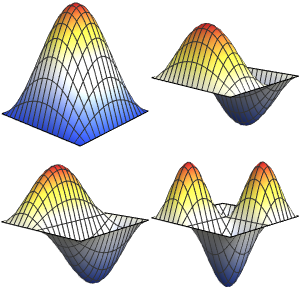
Visualisieren Sie die Eigenfunktionen.

Den kompletten Wolfram Language-Input zeigen

In[5]:=

ImageCollage[
 Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 
    ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, 
    PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ 
  funs, Background -> Transparent]

Out[5]=