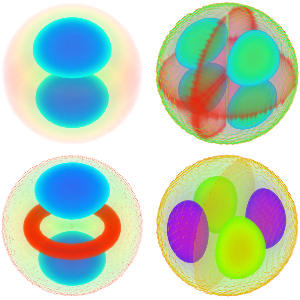
Eine Eigenfunktionen-Galerie für den Laplace-Operator in einer Kugel erzeugen

Definieren Sie einen 3D-Laplace-Operator.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];

Spezifizieren Sie homogene Dirichlet-Randbedingungen.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];

Ermitteln Sie die 16 kleinsten Eigenwerte und Eigenfunktionen in einer Kugel.

In[3]:=

\[CapitalOmega] = Ball[{0, 0, 0}, 2];

In[4]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 16];

Die eigenwerte sind in den Termen der BesselJZero gegeben.

In[5]:=

vals[[1]] // TraditionalForm

Out[5]//TraditionalForm=

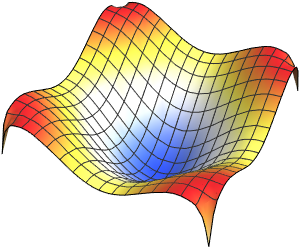
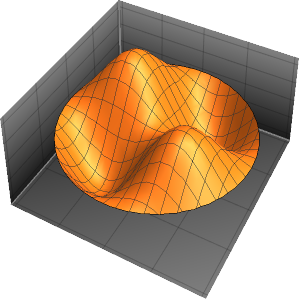
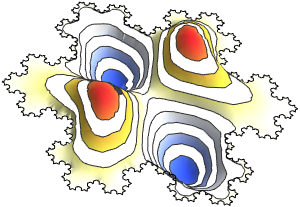
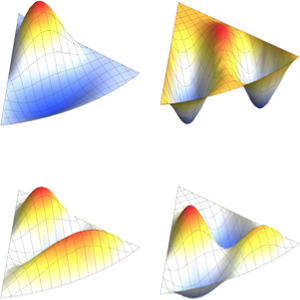
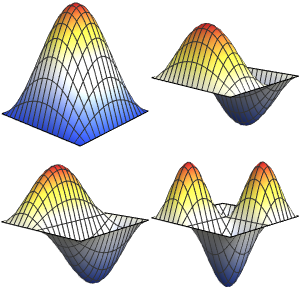
Generieren Sie eine Galerie der EIgenfunktionen.

In[6]:=

Grid[Partition[ ParallelTable[ DensityPlot3D[ funs[[i]] // N // Evaluate, {x, y, z} \[Element] \[CapitalOmega], Boxed -> False, Axes -> False, ColorFunction -> Hue, Method -> {"ShrinkWrap" -> True}, ImageSize -> 125], {i, 16}], 4]]

Out[6]=