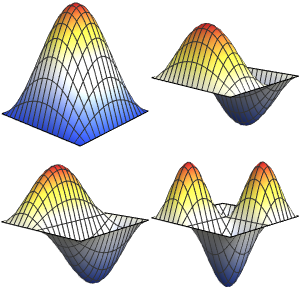
Eine Eigenfunktionserweiterung generieren
Berechnen Sie die Eigenfunktionserweiterung der Funktion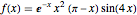 
bezüglich der Basis gegeben durch einen Laplace-Operator mit Dirichlet-Randbedingungen auf dem Intervall 
.
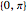In[1]:=
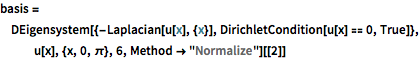
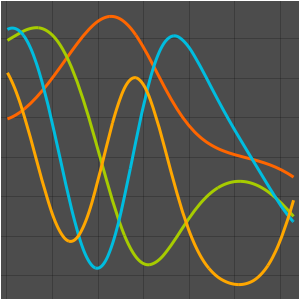
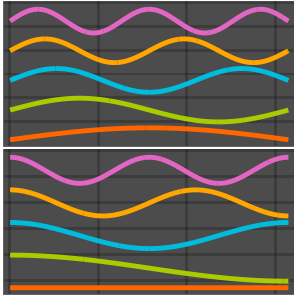
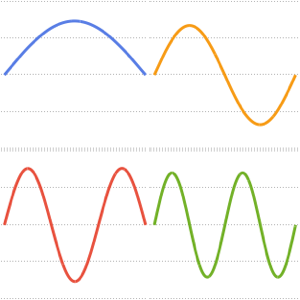
basis = DEigensystem[{-Laplacian[u[x], {x}],
DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6,
Method -> "Normalize"][[2]]Out[1]=
Berechnen Sie die Fourier-Koeffizienten für die Funktion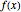 
.
In[2]:=
f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]In[3]:=
coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] //
FullSimplify);Bestimmen Sie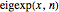 
als die 
Partialsumme der Erweiterung.
In[4]:=
eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]In[5]:=
eigexp[x, 3] // NOut[5]=
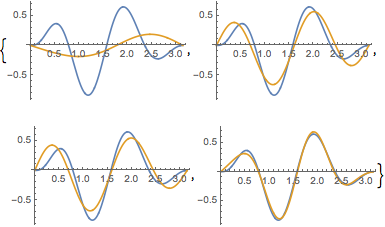
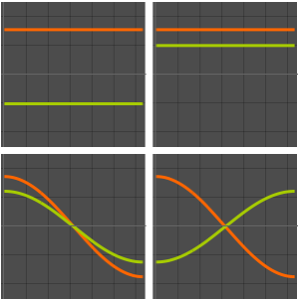
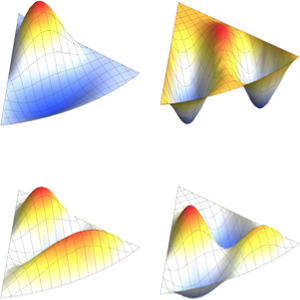
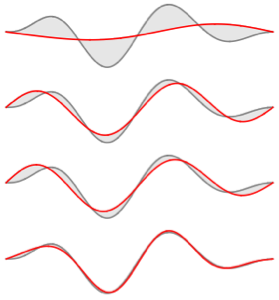
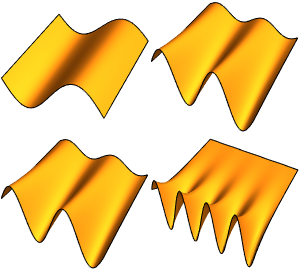
Vergleichen Sie die Funktion mit ihrer Eigenfunktionserweiterung für verschiedene Werte von 
.
In[6]:=
Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]Out[6]=
