Wolfram Language™

Eigenfunktionen für eine eingespannte Membran berechnen

Berechnen Sie die sechs ersten Eigenfunktionen für eine runde Membran mit eingespannten Rändern.

Spezifizieren Sie einen Laplace-Operator.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

Spezifizieren Sie eine Dirichle-Randbedingung.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Ermitteln Sie die sechs kleinsten Eigenwerte und Eigenfunktionen.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] Disk[], 6];

Untersuchen Sie die Eigenwerte.

In[4]:=

vals

Out[4]=

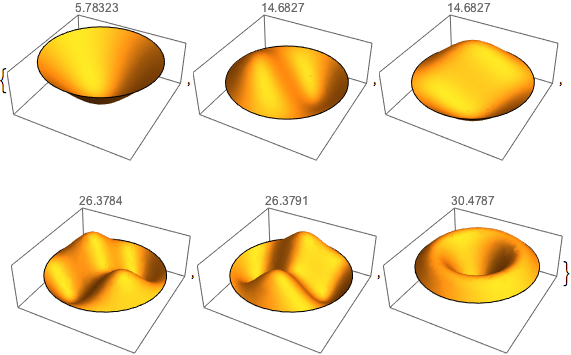
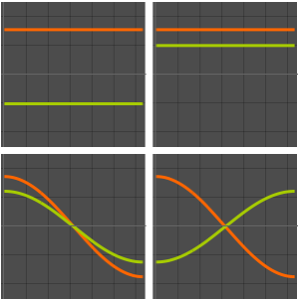
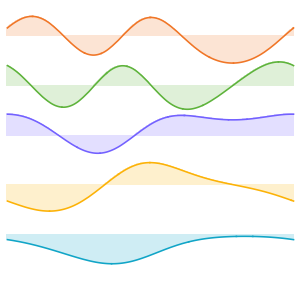
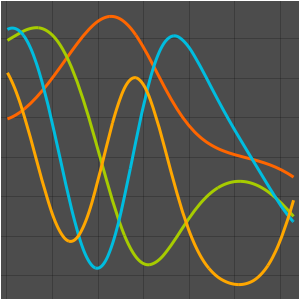
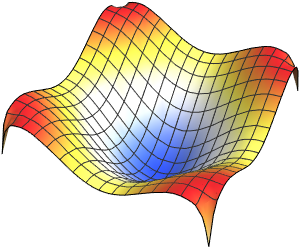
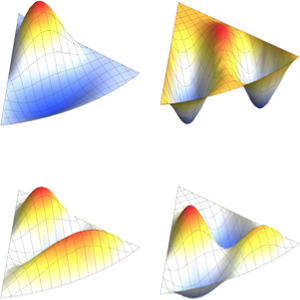
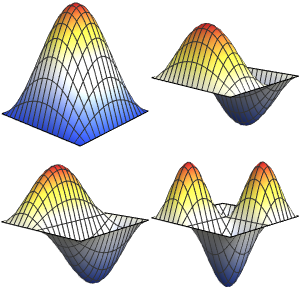
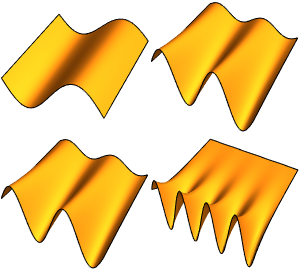
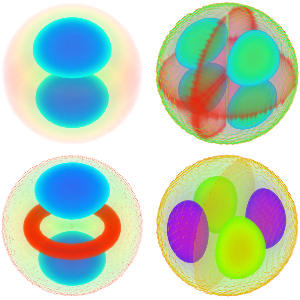
Visualisieren Sie die Eigenfunktionen.

In[5]:=

Table[Plot3D[funs[[i]], {x, y} \[Element] Disk[], PlotRange -> All, PlotLabel -> vals[[i]], PlotTheme -> "Minimal"], {i, Length[vals]}]

Out[5]=