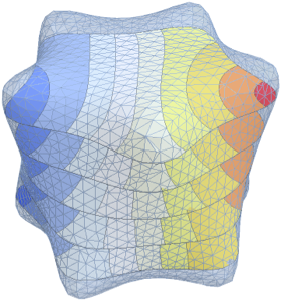
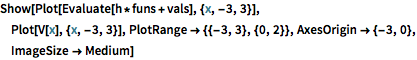Das Spektrum eines Schrödinger-Operators bestimmen

Lösen Sie das Eigenproblem einer Schrödinger-Gleichung 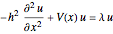über einer eindimensionalen Region.

Bestimmen Sie einen Schrödinger-Operator ohne Nebenbedingungen.

In[1]:=

h = 1/10; V[x_] := x^2 \[ScriptCapitalL] = -h^2*u''[x] + V[x]*u[x];

Berechnen Sie die 10 kleinsten Eigenwerte und Eigenfunktionen auf einem verfeinerten Gitternetz.

In[2]:=

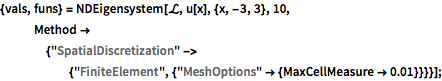
{vals, funs} = NDEigensystem[\[ScriptCapitalL], u[x], {x, -3, 3}, 10, Method -> {"SpatialDiscretization" -> {"FiniteElement", \ {"MeshOptions" -> {MaxCellMeasure -> 0.01}}}}];

Untersuchen Sie die Eigenwerte.

In[3]:=

vals

Out[3]=

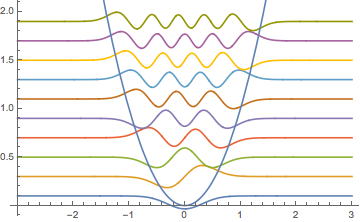
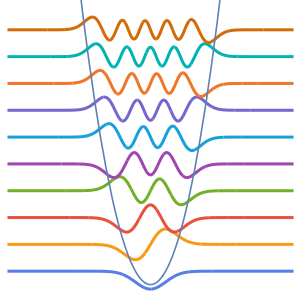
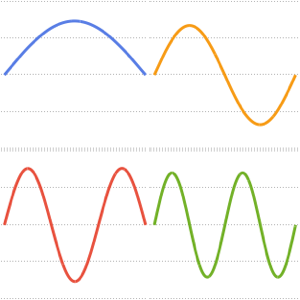
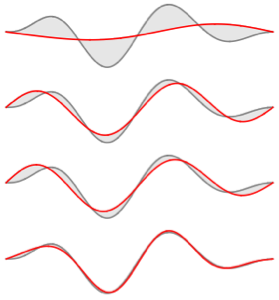
Visualisieren Sie die Eigenfunktionen mit Skalierungsfaktor 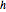und versetzt um die entsprechenden Eigenwerte.

In[4]:=

Show[Plot[Evaluate[h*funs + vals], {x, -3, 3}], Plot[V[x], {x, -3, 3}], PlotRange -> {{-3, 3}, {0, 2}}, AxesOrigin -> {-3, 0}, ImageSize -> Medium]

Out[4]=